using KaTeX

Original author: Michal Švagr
Maintaner: Filip Štěpánek

Citát
Ano je to těžké, ale život je těžký.
prof. Dr. Ing. Zdeněk Hanzálek (2021)

KO

ILP

• $x$ a $y$ - proměnné řešení
• $l$ - pomocné reálné proměnné
• $k$ - pomocné celočíselné proměnné
• $z$ - pomocné binární proměnné
• $M$ - velké číslo
• Absolutní hodnota $|x-y|$
  • $x-y\le l$
  • $y-x\le l$
• Absolutní hodnota $|x+y|$
  • $x+y\le l$
  • $-x-y\le l$
• Liché číslo
  • $x=2k+1$
• AND
  • $x+y\ge2$
• OR
  • $x+y\ge1$
• XOR
  • $x+y=1$
• $x\implies y$ (Implikace)
  • $x\le y$
• $\min(x_i)$
  • $l\le x_i \qquad \forall i \in n$
• Vypínání
  • vybírání ze dvou:
    • $x<1+M(1-z)$ - zapnutá při $z=1$
    • $1\le x+M(z)$
  • vybírání z více:
    • $\sum^n_{i=1}z_i=2$ - přesně dvě (znaménko dle potřeby)
    • $x_j<1+M(1-z_i)$

SP

• SP (Shortest Path)- nejkratší cesta z $a$ do $b$
• SPT (Shortest Path Tree) - nejkratší cesty z $a$ do všech ostatních (out-tree)
• In-tree - nejkratší cesty ze všech do jednoho bodu (otočíme hrany v SPT)
• All Pair Shortest Path - nejkratší cesty mezi všemi vrcholy
• Nejdelší cesta - obrátíme ceny hran
• Když maj nody váhy - rozdvojím je a vytvořím orintovanou hranu s váhou
• MST (Minimal Spaning Tree) - nejlevnější propojení všech nodů
  • Je rozdíl, když dělám MST a SPT! Cesty jsou často různé
• Steiner Tree - nejlevnější propojení vysílače s příjmači v síty
• Nalézt SP v grafu se zápornými cykli je NP-hard
• Bellman-Ford a Floy podporují negativní hrany
• Sled (Edge progression) - posloupnost vrcholů a hran
• Cesta (Path) - neopakují se ani vrcholy ani hrany
  • Když nejsou negativní cykly - nejkratší sled je i nejkratší cesta
  • Když nejsou negativní váhy - nejkratší sled obsahuje i nejkratší cestu
• $n$ - počet vrcholů
• $m$ - počet hrans

Troúhelníková nerovnost

• $l$ je suma cen v nejkratší cestě
• $c$ je suma cen v cestě
• Platí, že:
  • $l(i,j) \leq l(i,k) + l(k,j)$
  • $l(i, j) \leq c(i, j)$
  • $l(i, j) \leq l(i, k) + c(k, j)$
  • $l(i, j) \leq c(i, k) + l(k, j)$
    

Negativní cykly

• Rozbijí nám algoritmy
• Proto je nejkratší cesta s negaitvními cykly NP-Hard
• Pozor musíme dávat, když otáčíme ceny pro problém nejdelších cest
• Důkaz:
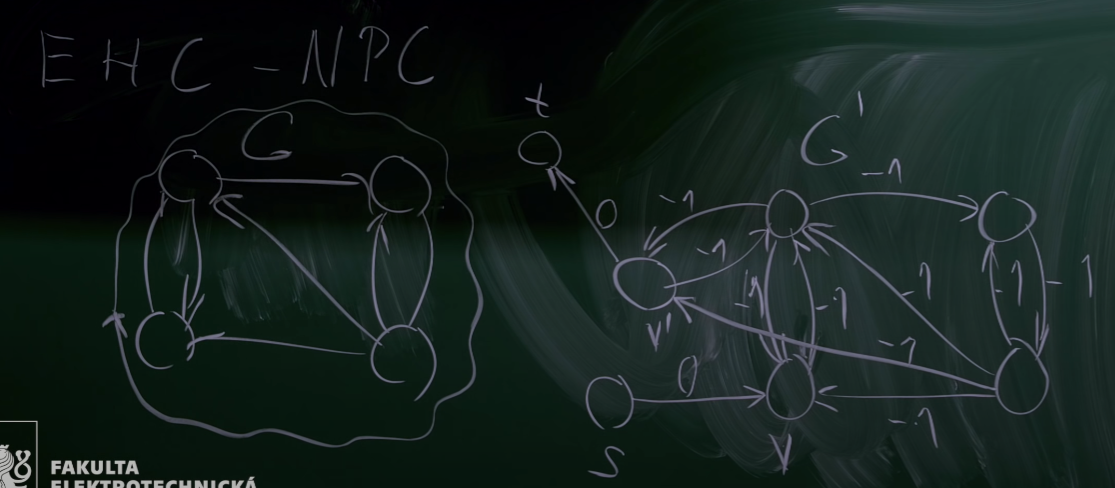
  • Dokazujeme přes redukci existence hamiltonovksého cyklu (EHC) na STP
  • EHC = Máme orientovaný graf s cykly a hledáme cyklusm který prochází všemi vrcholy právě jednou
  • Postup redukce:
    1. Zkopírujeme graf G a přidáme všem hranám váhu -1
    2. Zduplikujeme libovolný vrchol $v$ a zkopírujeme i jeho hrany k novému vrcholu
    3. Přidáme zdrojový vrchol $s$ a propojíme ho s vrcholem $v$ s cenou 0
    4. Přidáme cílový vrchol $t$ a propojíme ho s kopiíí vrcholu $v'$ s cenou 0
       

Bellmanův princip optimality

• Jestliže máme nekratší cestu z $a$ do $b$ přes $k$ pak cesta z $a$ do $k$ je také nejkratší stejně tak z $k$ do $b$
• Belmanova rovnice je trojůhelníková nerovnost s cenami cestami $c$ místo vzdáleností $l$
• Jinými slovy, nejkratší cesta se skládá ze segmentů nejkratších cest
  
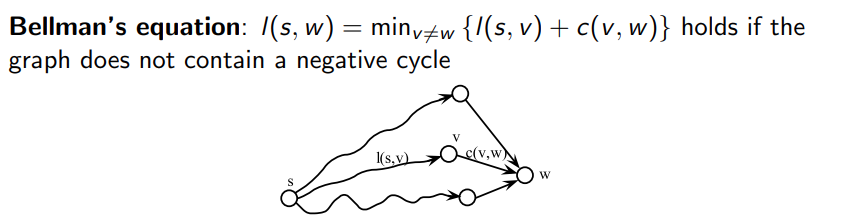
• Důkaz sporem:
  1. • Máme nejkratší cestu z $P_k=(s,w)$, která vede přes $v$, tak, že existují hrany $e=(v,w)$ a $P_{k-1}=(s,v)$
     • Uvažujme cestu $Q_1 = (s,v)$ takovou, že její cena je menší než cena cesty (v,w)
     • To je spor s tvrzením, že $P_k=(s,w)$ je nejkratší cesta
  2. (tohle je možná blbě)
     • Uvažme další cestu $Q_2 = (s,v)$, která prochází skrze $w$ takovou, že její cesta je kratší než cesta $P_{k-1}$
     • To je opět spor s tím, že $P_k=(s,w)$ je nejrkatší cesta
       

Algorithm for DAGs

• Skoro jako Bellman-ford
• Vrcholy očíslujeme tak aby menší vždy ukazoval jen na větší
• Postupně bereme vrcholy od prvního po poslední
• Využíváme vlastnosti, že vše co je předemnou už má minimum, takže stačí koukat jen na hrany co do mě vstupují

Dijkstra Algorithm

• Pouze nezáporné ceny hran
• $O(n^2)$ nebo s priority queue $O(m + n \log n)$
• algo:
  1. V grafu vrcholům přiřadím hodnotu $\infty$ a startu hodnotu 0
  2. Založíme množinu $R$ což je množina, ve které jsou nejkratší cesty
  3. Vybereme z množini vrcholů mimo $R$ ten s nejmenší hodnotou a vložíme ho do $R$
  4. Pro všechny hrany $\overrightarrow{AB}$ vystupující z $R$ nastavíme hodnotu vrcholů $B$ na opačné straně hrany (mimo $R$) na $\min$(původní hodnota $B$, hodnota $A$ + cena hrany)
  5. Pokud existuje vrchol mimo množinu $R$ $\to$ vracíme se do bodu 3
• Příklad: https://youtu.be/LCTwYILbmEY?t=991
• Důkaz (indukcí):
  • Pro $|R|=1$ tak platí minimum, protože je tam jen start za cenu 0
  • Pomocí belmana dokážu, že vrchol, který přidávám do $R$ je segmentem nejkratší cesty
  • Jinými slovy, mám nejkratší cestu $(s,v)$ a přidávám vrchol $w$, protože má ze všech možných cest z $v$ nejmenší cenu. Proto vzniklá cesta $(s,w)$ je opět nejkratší protože neexistují hrany se zápornou váhou.
  • https://youtu.be/LCTwYILbmEY?t=1658
  • Raději přijládám slide z přednášky
    

A*

• Když hledáme jen cestu z bodu $s$ do bodu $t$ můžeme ji zrychlit tak, že ukončíme vyhledávání, když dorazíme do bodu $t$
• Navíc můžeme přidat další informace (informed search), “jakým směrem” se bod $t$ nachází

Bellman-Ford Algorithm

• Umí detekovat záporné cykly (ve vnitřní smyčce kontrolujeme trojúhelníkovou nerovnost)
• $O(n*m)$
• Lze řešit dynamickým programováním
• Algoritmus:
  1. V grafu vrcholům přiřadím hodnotu $\infty$ a startu hodnotu 0
  2. Naincializuji si $i=1$
  3. Projdu všechny hrany $\overrightarrow{AB}$ v grafu a vždy s zeptám zda nezlepším $B$ pomocí hodnoty $A$ + ceny hrany $\overrightarrow{AB}$
  4. Zvětším $i$ = $i+1$
  5. Pokud $i<n$ (kde $n$ je počet vrcholů) a zároveň jsem v bodě 3 vylepšil alespoň jednu hranu $\to$ vracím se do bodu 3
• Příkald 1: https://youtu.be/LCTwYILbmEY?t=6558
• Příklad 2: https://youtu.be/LCTwYILbmEY?t=7823
• Důkaz (indukce):

  • Vychází z Bellmanova principu optimality

  • Po prvním kroku (vnější smyčky) budu mít nejkratší cestu do vrcholu $v$ $\le$ nejkratší cestě s 1 hranou $(s,v)$

  • Každá další krok tento vztah stále platí jen se zvyšuje počet hran a to právě z bellmana

  • Platí $l_k(w)\leq c(E(P_k))$

    • $l_k(w)$ je label vrcholu $w$ po $k$ iteracích
    • $P_k$ je nejkratší možná cesta s maximálně $k$ hranami
    • $c(E(P_k))$ je cena cesty

  • https://youtu.be/LCTwYILbmEY?t=6967

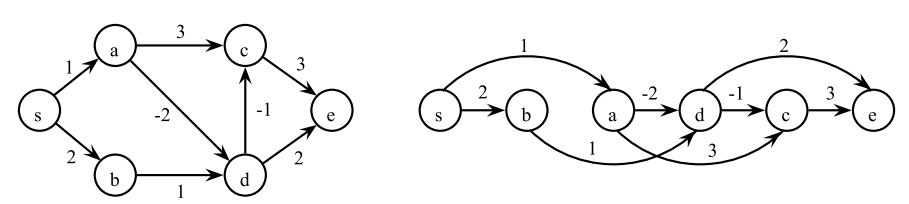
DAG

• Directed acyclic graph
• Graf můžeme topologicky uspořádat tak, že vždycky ukazuje pouze na následníky, nikoli na předky
• Užitečné například pro časové osy
• Můžeme efektivně procháze modifikovaným Bellman-Fordem v lineárním čase
• Složitost $O(|V|+|E|)$
  

Floyd Algorithm

• Umí detekovat záporné cykly (na diagonále $l_{ii}$ se objeví záporné číslo)
• Na diagonále máme nejkratší cykly, které procházejí daným vrcholem
• $O(n^3)$
• Hledá All Pair Shortest Path
• Algoritmus:
  1. Nainicializujeme matici $n*n$ s hodnotami $l_{ij}$ dle vah hran, na diagonále $0$ a zbytek $\infin$
  2. Nainicializujeme matici $n*n$ s hodnotami $p_{ij}=i$ matice parentů
  3. Máme 3 vnořené smyčky od 1 do $n$ s proměnnými $k$ (vnější), $i$ (prostřední) a $j$ (vnitřní)
  4. V uplně vnitřní smyčce máme podmínku na zlepšení pokud $l_{ij}>l_{ik}+l_{kj}$ pak nastavíme $l_{ij}=l_{ik}+l_{kj}$ a $p_{ij}=p_{kj}$
• Příklad: https://youtu.be/eFLIzXDeJ6U?t=3518

Johnson’s algorithm

• Počítá All Pair Shortest Path
• Dobrý na řídké grafy
• Kombinuje Dijkstru a Bellman-Ford
• $O(n*m*\log n)$

FLOW

https://rtime.ciirc.cvut.cz/~hanzalek/KO/Flows_e.pdf

• Zadáno jako (G, l, u, s, t):
  • G - orientovaný graf
  • l - lower bound hran
  • u - upper bound hran
  • s - startovní vrchol
  • t - koncový vrchol
• Co vteče musí vytéct z vrcholu - 1. Kirchoffův zákon
• Max flow - maximalizuje bilanci s

LP zadání

Balance

• Hodnota na vrcholu
• Spočítaná jako flow výstupní hran - flow vstupních
• Součet: balance + flow vstupní hran - flow výstupních = 0
• s má balanci > 0 a t balanci < 0
• Součet všech balancí v grafu je 0

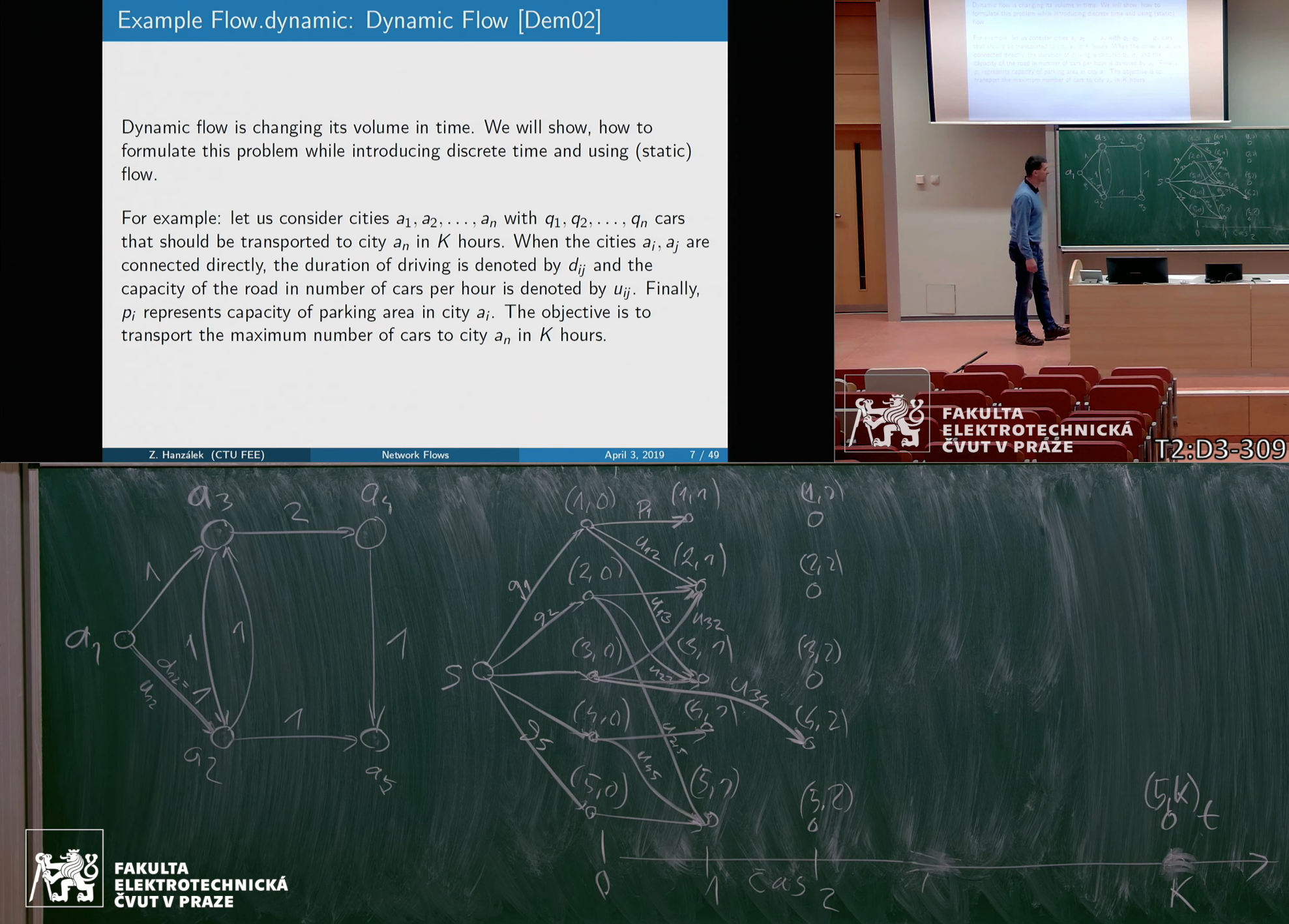
Dynamické flow
- Můžeme přidat čas
- Chceme kumulovat tok na nodech (např. ropa v tankerech, parkoviště)
- Lze převést zpět na max flow (zavedením duplicitních nodů v různých časech)

Min-cut

• Může existovat více ekvivalentních cutů
• Množina vrcholů obsahující s ale nikoliv t
• Hrany vedoucí z množiny cutu jsou plně sarurované ( flow = u ) a hrany vedoucí do množiny jsou také plně saturované ( flow = l )
• Kapacita cutu = maximální flow

Ford-Fulkerson (Max-Flow)

• Obecně řečeno nestačí maximalizovat všechny toky hrany, musíme na to jít chytřeji (nechceme např. maximallizovat hranu vedoucí do s) => proto Ford-Fulkerson

1. Vytvoření proveditelného toku
   • Pokud jsou všechny lower boundy nulové, neboli ∀e ∈ E(G); l(e) = 0 můžu jít do kroku 2. s initial flow = 0
   • Pokud nejsou všechny lower-boundy nulové:
     • Vytvoříme cirkulaci (vytvoříme hranu z t do s s l=0 a u=∞)
     • Spočítám balance (pozor, tyto balance jsou odlišné od výše zmíněných!) (l vstupních - l výstupních) a snížím hodnoty l a u o l
     • Přidám nový s’ od kterého povedeme hrany do vrcholů s balancí > 0 s l = 0 a u = balanci
     • Přidám nový t’ do kterého povedeme hrany z vrcholů s balancí < 0 s l = 0 a u = -balanci
     • Zapnu max-flow na novém grafu
     • Výsledné new-flow zadám do starého grafu jako flow = l + new-flow
2. Inkrementální zlepšování
   • Nejdříve najdeme cestu od s do t takovou, že každá hrana v cestě není plně saturovaná (je možná použít zpetné hrany)
   • Této cestě zvýšíme (snížíme v opačných hranách) tok o maximální možné zlepšení (min z možných zlepšení jednotlivých hran cesty)
   • Opakuji dokud jsem ještě schopen najít zlepšující cestu z s do t

• Time complexity:
  • Celočíselné flow (znamená celočíselné l a u)
    • obecně - O(|E|² * U) kde U je maximum z u
  • Alternativně použijeme algoritmus Floyd-Warshall
    • Při vytváření augmentované cesty použijeme algoritmus pro nejkratší cestu - O(|E|² * |V|)

Celočíslenost Ford-Fulkersona

• Když všechny kapacity l a u jsou celá čísla (integery), kapacita augmentované cesty γ při běhu Forda-Fulekrsona je rovněž celé číslo
• Protože máme nax-flow konečné hodnoty, existuje konečný počet kroků algoritmu
• Rovněž z LP formulace můžeme říci, že celočíselnost vyplývá z úplné unimodularity matice incidence grafu G, což je matice A ve formulaci A - x ≤ b.

Feasible Flow with Balances

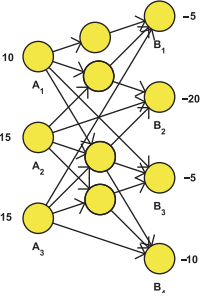
• Zadáno jako (G, l, u, b):
  • G - orientovaný graf
  • l - lower bound hran
  • u - upper bound hran
  • b - balance vrcholů (suma všech balancí = 0)
• Derivát tokové sítě, ale máme více zdrojů a více cílů
• Decision problém - ptáme se, jestli lze dosáhnout toku
• Tento problém lze polynomiálně redukovat na problém mac flow
  1. Přidáme nový zdroj s’ a spojíme ho s původními zdroji a nastavíme l=u=b (jinými slovy nastavíme lower bound a upper bound na balanci uzlu)
  2. Přidáme společný spotřebič t’ a spojíme ho s původními spotřebiči a nastavíme l-u-b (jinými slovy nastavíme lower bound a upper bound na balanci uzlu)
  3. Pokusíme se vyřešit max-flow.
  4. Existují-li toky pak lze použít zadané balance a rozhodovací úloha má odpověď ano.

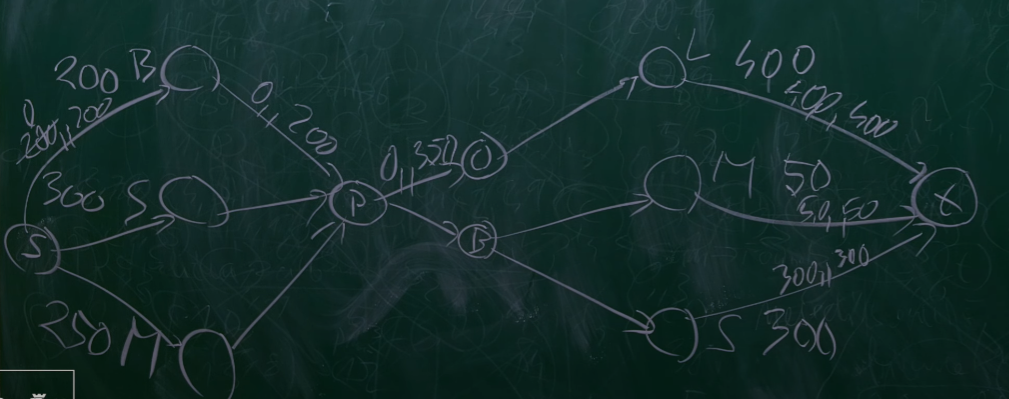
Minimum cost flow

• Každá hrana má cenu c
• Přenesení jedné jednotky po dané hraně nás stojí právě c
• Hledáme maximální tok při minimálním costu
• Zadáno jako (G, l, u, c, b):
  • G - orientovaný graf
  • l - lower bound hran
  • u - upper bound hran
  • c - cost hran
  • b - balance vrcholů (suma všech balancí = 0)
    
• Max flow můžeme polinomiálně redukovat na minimum cost flow
  1. Přidáme cirkulaci = přidáme hranu z t do s, kde u=∞ a l=0 a c=-1
  2. Cenu všech ostatních hran c nastavíme na 0
  3. Balanci všech vrcholů b nastavíme na 0
  4. Maximalizujeme cenu
• Shortest path můžeme polynomiálně redukovat na min cost flow
  1. Použijeme LP formulaci min-cost flow
  2. Nastavíme b(s)=1 a b(t)=-1
  3. Pro všechny ostatní (t.j. mimo zdroj a spotřebič) b(v)=0
  4. l(e)=0 a u(e)=∞ pro všechny hrany e
  5. Získáte (primární) LP formulaci problému nejkratší cesty (viz příklad zcela unimodulární matice A v přednášce o ILP) #Tady nemám sebemenší tušení co tohle znamená, lol
• Chinese mailman problem můžeme polynomiálně redukovat na min cost flow (#bylo to v testu, tak se na to nevykašlete 🙃)
  • Listonoš musí zajít na poštu, vzít dopisy a obejít s nimi všechny ulice města a nakonec se vrátit do výchozího bodu – zpět na poštu. Musí přitom urazit minimální vzdálenost.
  • V grafu, který reprezentuje město, představují hrany grafu ulice a uzly odpovídají křižovatkám. Hrany jsou ohodnoceny kladnými čísly, které odpovídají délce ulic.
  • Postup:
    1. Nastavíme b(v)=0 pro všechny vrcholy
    2. Nastavíme l(e)=1 a u(e)=∞ pro všechny hrany
    3. Vyřešíme min flow
  • Existuje pošťákova cesta, která využívá každou hranu přesně jednou (tj. Eulerian walk) iif pokud má každý vrchol stejný indegree a outdegree (tj. Eulerian digraph).

Cycle Canceling Algorithm (řeší Minimum cost flow)

1. Najdeme feasible flow graf
2. Vytvoříme residuální graf
   • Hrany v grafu zdvojíme
     • Dopředné hrany budou mít hodnoty u = u - flow a c = c
     • Zpětné hrany budou mít hodnoty u = flow - l a c = -c
   • Vyházím hrany s u = 0
3. Naleznu záporný cyklus (záproný součet cen)
   • γ = součet cen * min(u) v cyklu
   • Upravíme flows v původním grafu o γ aby to dávalo smysl (neporušil jsem kirchofa)
4. Znovu jdu do bodu 2. dokud existuje negativní cyklus v residuálním grafu

• Time complexity - $O(|E|^2 * |V| * C * U)$ kde U je maximum z u a C maximum z c

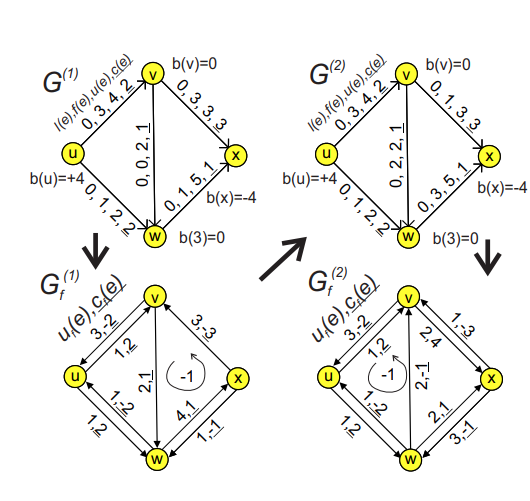
Minimum cost multicommodity flow

• Přidává různé typy přenášených informací (které nesmíme pomotat)
• Každý vrchol má balance jednotlivých typů
• Každý vrchol musí splňovat kirchofův zákon pro jednotlivé komodity
• • Zadáno jako (G, l, u, c, b1…m):
    • $G$ - orientovaný graf
    • $l$ - lower bound hran
    • $u$ - upper bound hran
    • $c$ - cost hran
    • $b[1..m]$ - vektor znázorňující balanci pro jednotlivé komodity (v součtu musí dávat 0 přes celý graf a komodity)
• Cíl minimalizovat $\sum_{e \epsilon E(G)}^{}\sum_{m\epsilon M} f^{m}(e)*c(e)$
  

Párování

• Maximum Cardinality Matching Problem
  • Párování s největším počtem hran (spojení)
  • Algo - M-alternig Path
    1. Najdeme náhodné párování
    2. Najdeme alternující cestu (cesta na které se střídá nevybraná hrana s vybranou, začíná a končí nevybranou hranou a koncové vrcholy nepatří žádnému párování)
    3. Prohodíme vybrané a nevybrané hrany v cestě
    4. Opakujeme 2-3 dokud neexistuje alternativní cesta
       
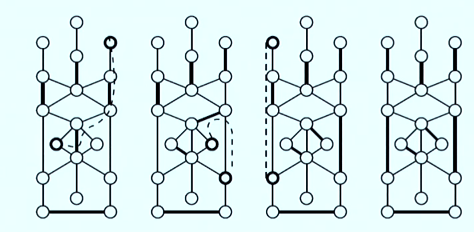
• Maximum Cardinality Matching in Bipartite Graphs
  • Párování s největším počtem hran (spojení) párující vrcholy ze dvou skupin
  • Lze řešit pomocí max-flow
    
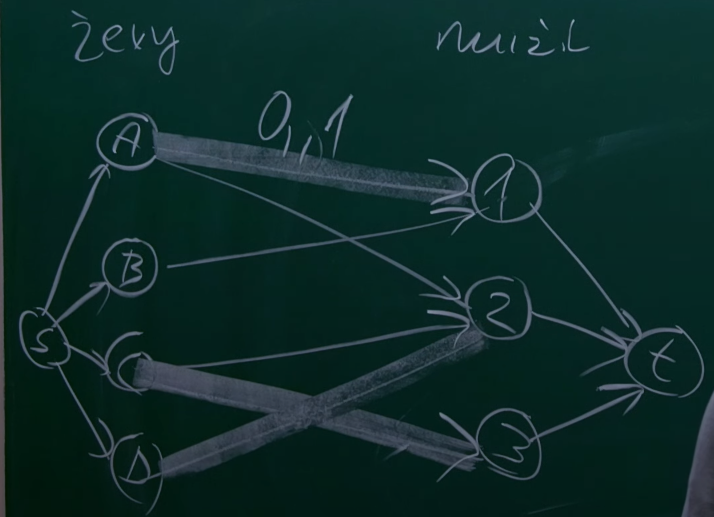
• Minimum Weight Matching in a weighted graph
  • Takové párování co nám dá nejmenší součet cen na hranách
• Minimum Weight Perfect Matching
  • Takové párování co nám dá nejmenší součet cen na hranách a všechny vrcholy jsou napárované
  • Známé jako assignment problem
  • Lze převést na min cost flow podobně jako bipartitní párování
    

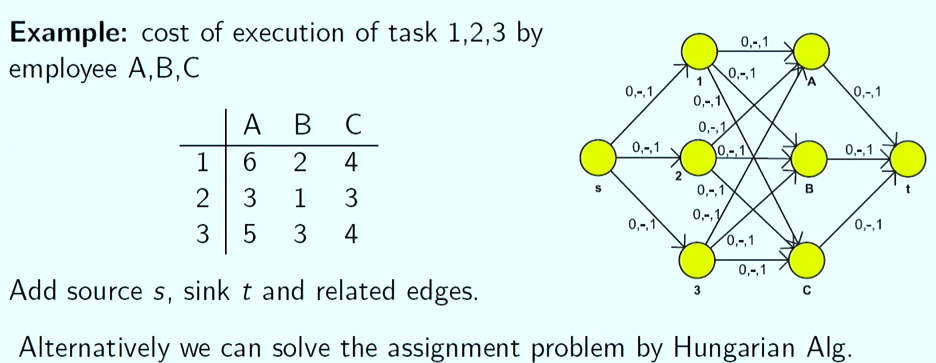
Knapsack

• NP-Hard, ale ne moc (existují kvalitní aproximační algoritmy)
• Je zadán jako:
  • $n$ = počet předmětů
  • $c_i$ = cena předmětu
  • $w_i$ = váha předmětu
  • $W$ = nosnost batohu (nesmí být překročena)
• předmět buď vložíme nebo nevložíme do batohu
• Maximalizujeme cenu věcí v batohu

Fractional Knapsack problem

-Stejné jako knapsack, ale předměty nemusíme vkládat celé

• Řeší: bin packing, contaner loading, 1-D, 2-D, 3-D cutting problem.
• $O(n\log n)$ jen znovu seřadím
• Algoritmus:
  1. Pokud $\sum_{i=1}^{n} w_i <W$ vložíme vše a máme hotvo
  2. Vyřadíme předměty s $w_i > W$
  3. Přeindexujeme předměty podle $\frac {c_i}{w_i}$ od největšího po nejmenší
  4. Postupně dáváme předměty do batohu dokud se nám tam další předmět nevejde celý
  5. Tento předmě označíme jako $h$
  6. Do batohu dáme takovou čás $h$, která se do něj ještě vejde

R-aproximační algoritmus

• Takový algoritmus $A$, který je definován číslem $r\in Q$ pro problém $J$
• Výsledek algoritmu $A$ je maxilmálně $\frac{1}{r}$ hodnoty optima algoritmu $J$
• Pro maximalizaci $J^A(I)\ge \frac{1}{r}*J^*(I)$
• Pro minimalizaci $r*J^*(I)\ge J^A(I)$
• Frekvence “worst case scenaria” není sledována

Knapsack (0/1 Knapsack)

2-Aproximation algorithm

• Alespoň $\frac {1}{r}$ optima (kde $r$=2)
• $O(n)$
• Algoritmus:
  1. Pokud $\sum_{i=1}^{n} w_i <W$ vložíme vše a máme hotvo
  2. Vyřadíme předměty s $w_i > W$
  3. Přeindexujeme předměty podle $\frac {c_i}{w_i}$ od největšího po nejmenší
  4. Postupně dáváme předměty do batohu dokud se nám tam další předmět nevejde celý
  5. Tento předmě označíme jako $h$
  6. vložíme předměty $\{1, ...\ ,h-1\}$ nebo jen $\{h\}$ na základě toho, co je výhodnější
• Důkaz, že $r=2$
  • Můžeme vynechat předměty, jejichž $w\gt W$
  • Když $\sum_{i=1}^{n}w_i\lt W$, tak máme optimální řešení
  • Protože $\sum_{i=1}^{h}c_i$ je horním omezením optimální hodnoty, lepší z dvou možných řešení $\{\sum_{i=1}^{h}c_i\}$ a ${h}$ je minimálně polovina optimální hodnoty
    • $J^A(I)=max\{\sum_{i=1}^{h-1}c_i, c_h\}\ge\frac{\sum_{i=1}^{h}c_i}{2}\ge\frac{1}{2}J^*(I)$

Dynamic programing

• Pseudopolynomiální
• $O(nC)$ kde $C$ je velmi veliké číslo
• 2 varianty: máme celočíselné ceny, máme celočíselné váhy
• Celočíselné hodnoty napíšeme do sloupců, řádky budou indexy předmětů pro vložení a hodnoty jsou neceločíselné valstnosti
• Tabulky: https://youtu.be/71B1FMVVX_o?t=7252
• Lze zmenšit počet sloupců (zrychlit algo) nalezením dělitele $t$ ve tvaru $\bar{c_j} = \lfloor \frac{c_j}{t} \rfloor$ (pokud se nejedná o společného dělitele snižujeme přesnost řešení)

Aproximační schéma

• $r = 1+\epsilon$
• Mějme zadaný knapsack a $\epsilon$ (o kolik jsme ochotni být vzdáleni od optima v procentech)
• $O(n^2*\frac{1}{\epsilon})$
• Postup:
  1. Spustíme 2-aproximační algoritmus a řešení označíme jako $S_1$
  2. Spočítáme proměnou $t=max\{1,\frac{\epsilon * c(S_1)}{n}\}$
  3. Spočítáme $c_j^{'} = |{\frac{c_j}{t}}|\ for\ j=1,...,n$
  4. Spustíme dynamické programování s pozměněnými cenami s upper boundem $C=\frac{2c(S_1)}{t}$
  5. Vrátíme vyšší cenu z $S_1$ a $S_2$

TSP

• Cesta v grafu přes všechny vrcholy grafu - Hamiltonovská cesta
• Spojení posledního a prvního vrcholu - Hamiltonovská kružnice
• Reálné problémy TSP: Capacitated Vehicle routing Problem, Time Windows, Pick-up and Delivery.
• EHC - existence hamiltonovské kružnice (circuit)
  • Existuje kružnice, která prochází všemi vrcholy právě jednou?
  • Neorintovaný graf (obecný)
  • Rozhodovací problém - NP-Complete
  • Podobně existence hamiltonovského cyklu - v orientovaném grafu
• TSP - traveling salesman problem
  • Naleznout hamiltonovskou kružnici s minimální váhou
  • Symetrické TSP - v neorientovaném grafu
  • Asymetrické TSP - v orientovaném grafu
  • Optimalizační problém - NP-Hard
    • Počet hamiltonovských kružnic = $\frac{(n-1)!}{2}$
    • Ale nevíme proč je to tak těžký (jakože to neví ani Hanzálek), MSTs je ještě víc

NP-Hard problémy

• NP-Hard problémy
  • Neumíme najít polynomiální algoritmy
  • Řešitelné pseudopolynomiálním algoritmem (e.g. dynamické programování)
  • Složitost se pronásobuje konstantou, která souvisí s nějakým parametrem grafu (e.g. součet vah objektů u Knapsacku)
• Silně NP-Hard problémy
  • Neumíme na ně najít pseudopolynomiální algoritmy (e.g. dynamické programování)
  • Nepomůže nám omezit parametry vstupu polynomem - stále zůstává NP-Hard

Důkaz, že TSP je silně NP-Hard

• Mějme:
  • $L = TSP$
  • $L_p = TSP\ s\ resktricí\ c(e) \in {1,2}$ (t.j. omezení na váhy hran 1 a 2)
• Dokazujeme, že i když takto omezíme váhy hran, problém je stále NP hard a proto je silně NP-Hard
• Použijeme polynomiální redukci z existence hamiltonovské kružnice
• Postup:
  • Vezmeme neoritovaný graf $G$ s $n$ vrcholy
  • V tom najdeme libovolnou hamiltonovskou kružnici $G'$
  • V grafu $G$ ohodnotíme každou hranu z $G'$ váhou 1 a ostatní hrany váhou 2
  • $G$ má hamiltonovskou kružnici iif optimální TSP řešení je rovno $n$
    

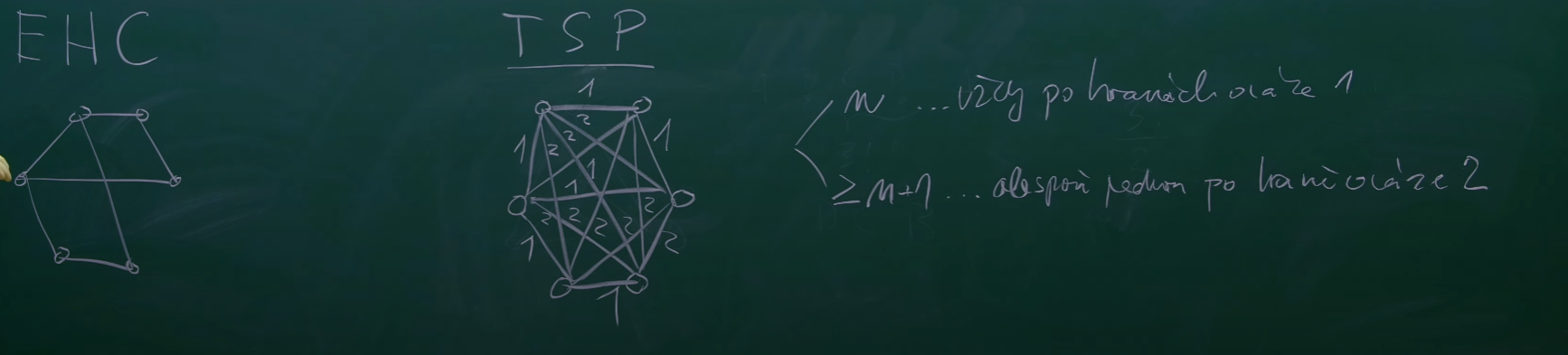
Obecný r-aproximační algoritmus

• Neexistuje n-aproximační algoritmus pro obecné TSP
• Důkaz sporem
• Uvažujme, že existuje r-aproximační algoritmus $\mathcal{A}$ s $r \ge 1$
• Ukážeme, že s tímto $\mathcal{A}$ jsme schopni řešit existenci hamiltonovské kružnice
• To by znamenalo, že $P=NP$
• Postup:
  • Mějme neorientovaný graf $G$, ve kterém chceme najít hamiltonovskou kružnici
  • Vytvoříme TSP instanci $K_n$ takovou, že vrcholy jsou totožné a hrany ohodnotíme:
    • $1$ pro hrany $\in G$
    • $2 + (r-1)*n$ pro hrany $\not\in G$
  • Vyřešíme pomocí $\mathcal{A}$
    • Pokud je optimum v intervalu $<n, r*n>$, pak Hamiltonovská kružnice existuje
    • Pokud je větší, G nemá hamiltonovský cyklus
  • To by znamenalo, že jsme schopni řešit EHC v polynomiálním čase algortimem $\mathcal{A}$
    

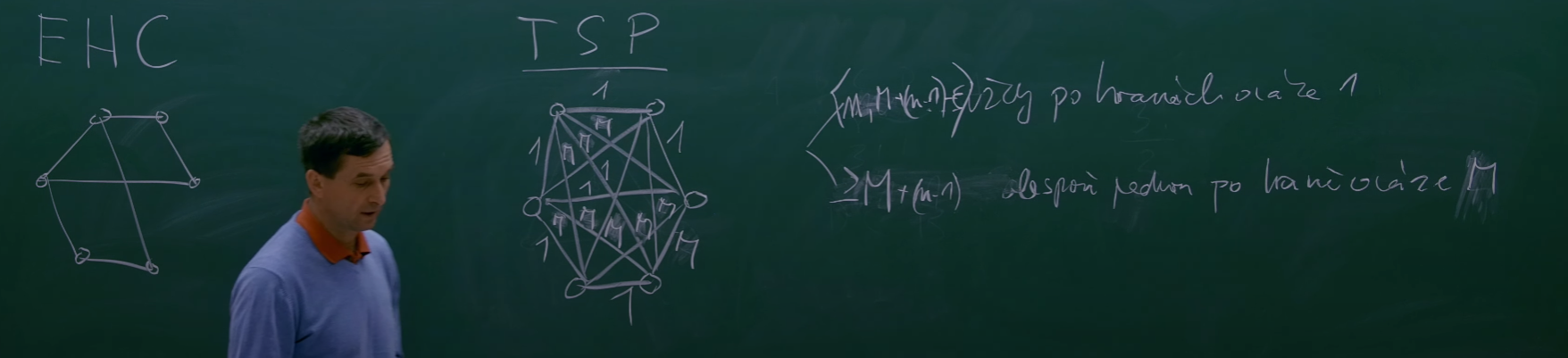
Metric TSP

• Má vlastnost, že platí trojůhelníková nerovnost $c(|\overrightarrow{AB}|) \le$ $c(|\overrightarrow{AC}|)+ c (|\overrightarrow{CB}|$)
• Nadále silně NP-hard
• Existují aproximační algoritmy
• Nemetrickou instanci můžeme pevést na metrickou přičtením největší váhy hrany ke všem hranám
  • To neporošuje přechozí důkaz, protože nalezené optimum pro transformovaný graf neodpovídá přesně původnímu grafu, protože je k němu přičteno “velké číslo” zatažené transformací

Nearest Neighbor

• $O(n^2)$
• Heuristika, nikoli aproximační algoritmus
• Postup:
  1. Vybereme první vrchol a přeindexujeme na $v_{[1]}$
  2. Vybereme nejlacinější hranu, která z nás vychází a nejde do vrcholů, ve kterých jsme už byli
  3. Opakujeme bod 2 dokud nemáme všechny vrcholy
  4. Spojíme poslední vrchol s $v_{[1]}$

Double-tree (metric TSP)

• 2-aproximační alog
• $O(n^2)$
• Algoritmus:
  1. Najdeme MST $T$
  2. Všchny hrany v $T$ zvojíme
  3. V $T$ nalezneme Eulerovský tah $L$
  4. Z Eulerovského tahu $L$ odebereme vrcholy co jsme už navštívili, ale ponecháme poslední a tím vytvoříme Hamilnovskou kružnici $H$
     • Příkald: https://youtu.be/p9qiafTnd6Q?t=3726
       • EuT = ABCBADAEA
       • TSP = ABCDEA
• Důkaz faktoru $r=2$:
  1. Protozože v grafu platí troúhelníková nerovnost, vynechané hrany nemůžou prodloužit cestu, $c(E(L)) \ge c(E(H))$ ($H$ může používat zkratky, které nejsou v $L$)
  2. Když smažeme jednu hranu v kružnici, vytvoříme strom. Proto platí nerovnost $OPT(K_n,c) \ge c(E(T))$ (cena kružnice $\ge$ cena MST)
  3. Platí $2*c(E(T))=c(E(L))$ protože tvoříme $L$ zdvojením hran v $T$
  • Z toho vyvozujeme, že $2*OPT(K_n,c) \ge c(E(H))$
    • protože $2*OPT(K_n,c)\ge^{2.}2*c(E(T))=^{3.}c(E(L))\ge^{1.}c(E(H))$

Christofides Algorithm (metric TSP)

• $\frac{3}{2}$-aproximační algo
• $O(n^3)$
• Algoritmus:
  1. Najdeme MST $T$
  2. Najdeme množinu $W$ = vrcholům s lichým stupněm z $T$ (bude jich sudý počet)
  3. V množině $W$ najdemme Minimum weight matching $M$ a tyto hrany přidáme do $T$
  4. Najdeme Eulerovský tah $L$ v upraveném MST
  5. z Eulerovského tahu odebereme vrcholy co jsme už navštívili, ale ponecháme poslední a tím získáme hamiltnovskou kružnici $H$
• Příkald (pravá část tabule): https://youtu.be/p9qiafTnd6Q?t=4615
• Důkaz faktoru $r=\frac{3}{2}$:
  1. Protozože v grafu platí troúhelníková nerovnost, vynechané hrany nemůžou prodloužit cestu, $c(E(L)) \ge c(E(H))$ ($H$ může používat zkratky, které nejsou v $L$)
  2. Když smažeme jednu hranu v kružnici, vytvoříme strom. Proto platí nerovnost $OPT(K_n,c) \ge c(E(T))$ (cena kružnice $\ge$ cena MST)
  3. Protože perfektní párování $M$ používá každou druhou hranu ve střídajiící cestě a protože je to párování s minimální vahou, tak vybere menší polovinu
     • $\frac{OPT(K_n),c}{2}\ge c(E(M))$
       
  4. Tvorba $L$ zaručuje $c(E(M))+c(E(T))=c(E(L))$
• Z toho získáme $\frac{3}{2}*OPT(K_n, c) \ge^{2.,3.} c(E(T)) + c(E(M)) =^{4.} c(E(L)) \ge^{1.} c(E(H))$

Tour improvement Heuristic - local seach k-OPT

1. Máme nějakou Hemiltonovskou kružnici
2. Smažeme $k$ hran
3. Propojíme oddělené tahy novými $k$ hranami tak aby opět vznikla Hemiltonovská kružnice
4. Zkontrolujeme zlepšení (nastavitelné kritérium), pokud nezlepšuje => změnu zahodíme

Scheduling

Dáváme všechny tásky zdrojům v čase.

• Pokud se jeden task nevejde mezi relase a deadline je úloha infeasible
• Každá úloha se musí provést
• Můžeme minimalizovat čas (cost) dokončení $C_{max}$ nebo spoždění (lateness) $L_{max}$
• Off-line - známe všechny tasky na začátku
• On-line - postupně nám tasky přicházejí
• Každá task může být v jednu dobu zpracováván jen jedním zdrojem
• Každá zdroj vykonává v jednu dobu max jednu úlohu
• Terminologie:
  • $T_i$ - úloha
  • $m$ typů zdrojů s kapactiou $R_k$
• Parametry:
  • $r_j$ - release time
  • $p_j$ - procesing time
  • $d_j$ - due date
  • $\tilde{d_j}$ - deadline
  • $T_i \prec T_j$ - task $T_j$ nemůže začít dokud neskončí $T_i$
  • $pmtn$ - preemptive tasks
  • $prec$ - tasky jsou na sobě závislé
  • $tmpn$ - temporal constrains
  • $set\text{-} up$ - některé tasky musí mezi sebou mít prostor na set-up time
• Proměnné:
  • $s_j$ - start time
  • $C_j$ - completion time
  • $L_j$ - lateness $L_j$ = $C_j - d_j$
• Graham’s Notation
  • $\alpha |\beta |\gamma$ (příklad: $P2|r_j,\tilde{d_j}|C_{max}$)
    • $\alpha$ jsou zdroje
    • $\beta$ jsou vlastnosti tasky
    • $\gamma$ jsou kritéria řešení
      • $C_{max}$ - délka rozvrhu
      • $\sum{C_j}$ suma časů dokončení
      • $\sum{C_j *w_j}$ suma vážených časů dokončení
      • $L_{max}$ zpoždění

One resurce scheduling

---

• $\alpha$ = 1
• Nejrychleji dokončeno
  • $1|prec|C_{max}$ - easy (seřadím dle závislostí + naskládám za sebe)
  • $1||C_{max}$ - easy (naskádám za sebe)
  • $1|r_j|C_{max}$ - easy (od nejmenšího $r_j$)
  • $1|\tilde{d_j}|C_{max}$ - easy (od nejmenšího $\tilde{d_j}$)
  • $1|r_j,\tilde{d_j}|C_{max}$ - NP-hard (krome $p_j$=1 $\to$ easy)

Důjaz že je silně NP-Hard

• Redukce z 3-partion problému
• Mějme 3-Partition rozhodovací problém $I_{3P}=(A,B)$
  • Multiset $A$ $3m$ čísel $a_1,a_2,...,a_{3m}$ (velikost předmětů)
  • Kladné číslo $B$ (velikost košů) takové, že $\forall i \in \{1,2,...,3m\}$ platí $\frac{B}{4} \lt a_i \lt \frac{B}{2}$ a $\sum_{i=1}^{3m}a_i=m*B$
  • Ptáme se, jestli jsme schopni rozdělit přesně 3 přeměty do každého koše tak, že se přesně vejdou
• Vyrobíme $1|r_j,\tilde{d_j}|C_{max}$ rozvrhový problém $I_{SCH}$ , který se skládá ze $4*m$ úloh $T_j=(p_j,r_j,\tilde{d_j})$ takových, že:
  • $\forall j \in \{1,..,m\}:T_j=(1,(B+1)*(j-1),(B+1)*(j-1)+1)$; umělé tasky oddělující subsety
  • $\forall j \in \{i+1,..,4m\}:T_j=(a_i,0,\infin), i=j-m$; každý tento task $T_j$ odpovídá elementu $I_{3P}$

• Nejmenší doba čekání
  • $1||\sum{C_j}$ - easy (seřazené dle $p_j$ - SPT shortest processing time first)
  • $1||\sum{w_j C_j}$ - easy (seřazené dle $\frac{p_j}{w_j}$)
  • $1|r_j|\sum{C_j}$ - NP-hard
  • $1|pmtn, r_j|\sum{C_j}$ - easy (upravené seřazení dle $p_j$)
  • $1|pmtn, r_j|\sum{w_j C_j}$ - NP-hard
  • $1|\tilde{d_j}|\sum{C_j}$ - easy (upravené seřazení dle $p_j$)
  • $1|\tilde{d_j}|\sum{w_j C_j}$ - NP-hard
  • $1|prec|\sum{C_j}$ - NP-hard
• Nejmenší lateness (v $\beta$ je $d_j$, $L_{max}$ může být záporný)
  • $1||L_{max}$ - easy (nejdřívšjší $d_j$ první = EDD - earliest due date first)
  • $1|r_j|L_{max}$ - NP-hard
  • $1|r_j, p_j=1|L_{max}$ - easy (EDD)
  • $1|pmtn, r_j|L_{max}$ - easy (EDD Horn)
  • $1|pmtn, r_j, d_j=\tilde{d_j}|L_{max}$ - easy (EDD/EDF Horn)
  • $1|pmtn, prec, r_j, d_j=\tilde{d_j}|L_{max}$ - easy (převod na $\cancel{prec}$ a pak EDD/EDF)

Bratley’s Algorithm

• $1|r_j,\tilde{d_j}|C_{max}$
• $O(n!)$
• Algoritmus:
  • Začnu stromovou strukturu s $n$ levely ($n$=počtu tasků)
  • Root na levelu 0 je před vložením prvního tasku
  • Na level 1 zadávám první tasky, na levelu 2 zadávám druhé tásky ze zbytku, atd.
  • Pravidla pro ukončení větve:
    • Pokud mezi childy nodu, existuje child, který nedodrží deadline tasku $\to$ do nodu se nazanořuji
    • Jestliže jsem našel node, který dokončil všechny využité tasky před $r_i$ všech zbylích tasků, jsem v optimální větvi $\to$ stačí projít pouze childy tohoto nodu
    • Jestliže jsem našel řešení a test optimality říká true $\to$ skončím
    • Pokud moje rozpracované řešení má horší hodnotu než již nalezené řešení $\to$ nezanořuji se dál
• BRTP
  • Podmínky:
    • První úloha v rozvrhu musí začínat na svém release timu
    • Všechny úlohy běží bez “idlu”
    • $r_1 \le r_i \forall i=2...k$
  • Jestliže platí, pak je rozvrh optimální
  • BRTP není nezbytnou podmínkou optimality!! (tzn. rovrh může být optimální, ačkoli BRTP neplatí)
  • Důkaz (divný):
    • Poslední úloha nemůže být dokončena dříve
    • Pořadí předcházejích úloh není důležité
    • Žádná úloha nemůže být dokončena před $r_1$
    • Po $C_{max}$ není žádná další úloha
• příhlad https://youtu.be/idc516WZZ1I?t=5131

Branch and Bound with LP-bounding

• $1|prec|\sum{w_j C_j}$
• Branch and bound dokud nenajdu první řešení
• Poté mohu využít částečné řešení ve větvi a spustit LP na zbytek větve
• Výsledek LP ($J^{LP}$) bude lower bound zbytku ve větvi, tudíž pokud $J^{LP}$+částeční řešení větve > aktuálně nejlepší řešení $\to$ větev neprocházím
• Lze použít i jiný zpusob nalezení lower boundu

Horn’s algorithm

• $1|pmtn, r_j|L_{max}$
• řeší: Eareliest Due Date firts a Earliest Deadline First
• algo:
  1. najdu $t_1 =\min{(r_j)}$ kde $j$ jsou tasky
  2. do množiny $T'$ vložím tasky s $r_j=t_1$
  3. z množiny $T'$ vyberu task $T_a$ s $\min{(d_j)}$
  4. najdu $t_2 =\min{(r_j)}$ kde $j$ jsou zatím nevybrané tasky do $T'$ nebo $\infty$
  5. tasku $T_a$ pustím na zdroji (odečítu čas do přerušení od $p_a$)
  6. 2 možnosti přerušení:
     • pokud $T_a$ doběhlo $\to$ vracím se do bodu 3
     • pokud zdroj došl na čas $t_2$ $\to$ $t_1=t_2$ a vracím se do bodu 2
  7. algorithm končí když se provedly všechny tasky
• příklad: https://youtu.be/MjekjcErKPc?t=708

Chetto, Silly, Bouchentouf algorithm

• $1|pmtn, prec, r_j, d_j=\tilde{d_j}|L_{max}$
• pouze změní tasky aby se dal použít Horn
• $O(n)$
• algo:
  • posunout release daty:
    1. v grafu precedencí najdu tasky $T_a$, které na jiný nečekají
    2. jejich následovníkům $T_s$ nastavím release time na $\max(r_s, r_a+p_a)$
    3. v grafu precedencí najdu tasky $T_a$, které mají všechny své předchůdce upravené dle bodu 2
    4. dokud v bodě 3 najdu tasky $\to$ vracím se do bodu 2
  • posun dealinů:
    1. v grafu precedencí najdu tasky $T_a$, které nemají následovníky
    2. jejich předchůdcům $T_p$ nastavím deadline na $\min(d_p, d_a-p_a)$
    3. v grafu precedencí najdu tasky $T_a$, které mají všechny své následovníky upravené dle bodu 2
    4. dokud v bodě 3 najdu tasky $\to$ vracím se do bodu 2
• příklad: https://youtu.be/MjekjcErKPc?t=1874

Paralel identical resource scheduling

---

• $\alpha _1$ = P
• Nejrychleji dokončeno
  • $P2||C_{max}$ - NP-hard (stejné jako rozdělování lupu mezi dva lupiče)
  • $P|pmtn|C_{max}$ - easy (McNaughton)
  • $P|pmtn,r_j,\tilde{d_j}|-$ - easy (rozhodovcí max-flow)
  • $P|prec|C_{max}$ - NP-hard (LS-aproximation)
  • $P||C_{max}$ - NP-hard (LPT aproximation, dynamické programování)
  • $P|pmtn,prec|C_{max}$ - NP-hard (Muntz&Coffman’s level algorithm)

McNaughton

• $P|pmtn|C_{max}$
• $O(n)$
• algo:
  1. spočítám si $C^*_{max}=\max(\max(p_i),\frac{1}{R}\sum^n_1 p_i$)
  2. dávám tasky na zdroj
  3. pokud mi task přeteče $C^*_{max}$ vyberu další zdroj na který nejdříve vložím zbytek tasku co přetekl
  4. dokud nejsou využity všechny tasky $\to$ vracíme se do bodu 2
• příklad: https://youtu.be/MjekjcErKPc?t=3452

LS-aporximation - List scheduling

• $P|prec|C_{max}$
• $r=2-\frac{1}{R}$ kde $R$ je počet identických zdrojů
• algo:
  1. uspořádáme tásky do seznamu $L$
  2. vybereme zdroj $Z$ se zatím nejkratším vytížením (konec posledního tasku na zdroji $t_z$)
  3. vytvoříme seznam $S$ s tasky s nejmenším $a_i$ (availability time) ve stejném pořadí jako v $L$
  4. z $S$ vybereme první task $T_i$ a vložíme ho do $Z$ se startem v $\max(t_z, a_i)$
  5. dokud nejsou využity všechny tasky $\to$ vracíme se do bodu 2

LPT-aproximation - Longest procesing time first

• $P||C_{max}$
• $O(n \log n)$
• $r=\frac{4}{3}-\frac{1}{3R}$ kde $R$ je počet identických zdrojů
• $r=1+\frac{1}{k}-\frac{1}{kR}$ kde $R$ je počet identických zdrojů a $k$ počet tasků na zdroji, který skončí jako poslední
• LS-aproximation bez $prec$ a s $L$ seřazeným (v bodě 1) sestupně dle $p_i$

Rothkopf - dynamické programování ($P||C_{max}$)

• $O(n*UB^R)$ kde $R$ je počet identických zdrojů
• algo:
  1. vytvoříme $R$ rozměrnou tabulku $n^R$ s jedním True v počátku souřadnic
  2. vezmeme task $T_i$ ze zbylých tasků
  3. projedeme všechny buňky tabulky a hodnty true zkopírujeme na pozice v ose větší o $p_i$
  4. staré hodnoty z tabulky smažeme
  5. dokud nejsou vybrány všchny tasky $\to$ vracíme se do bodu 2
  6. vyhrává True v tabulce s nejmenší $\max(souřadnice\ osy\ j)$ kde $j$ jsou názvy os (a.k.a. nejkratší vzdálenost od počátku souřadnic k True)
• Příklad: https://youtu.be/MjekjcErKPc?t=5759

Muntz&Coffman’s level algorithm ($P|pmtn,prec|C_{max}$)

• $r=2-\frac{2}{R}$ kde $R$ je počet identických zdrojů
• $O(n^2)$
• algo:
  • otagujeme tasky levely
    1. nejdříve beru tasky $T'$, ze kterých v precedentím grafu už nic nevychází
    2. taskům $T'$ nastavím level = $p_i$
    3. vyberu předcházející tásky tásků z $T'$ a vytvořím nové $T'$ s těmito tasky
    4. levely tasků $T'$ nastavím jako level = $p_i+\max(level_{si})$ kde $level_{si}$ jsou levely následovníků
    5. dokud nejsou olevelovány všechny tasky $\to$ vracím se do bodu 3
  • schduling:
    1. do množiny $Z$ vložím tasky, které nemají nedokončené předchůdce (jsou available)
    2. z množiny $Z$ vyberu tasky s $\max(level_i)$ do množiny $S$
    3. všechny tasky z $S$ rozložíme rovnoměrně na zdroje (jeden task nesmí běžet na 2 zdrojích zároveň, ale více úloh se může o čas na zdroji podělit)
    4. pokud mi zbyli zdroje a tásky v $Z$ $\to$ vracím se do bodu 2
    5. spustíme zdroje
    6. zdroje přerušíme jakmile nějaký task na zdroji dožene level jiného tasku nebo se task dopočítá $\to$ všechny tásky vyndáme ze zdrojů a vracíme se do bodu 1
• příklad: https://youtu.be/MjekjcErKPc?t=7382

Project scheduling ($\alpha _1$ = PS) --------------------------------------------

• $temp$ - temporal constraints
• Nejrychleji dokončeno
  • $PS1|temp|C_{max}$ - NP-hard
  • $PSm,1|temp|C_{max}$ - NP-hard

Temporal Constraints

Máme-li úlohu $T_i$ a úlohu $T_j$ kde z $T_i$ do $T_j$ existuje hrana s hodnotou $l_{ij}$. Pak to znamená $s_j \ge s_i + l_{ij}$.

• Aby byl Schedule feasible v grafu musí být pouze záporné cykly
• převod z $PSm,1|temp|C_{max}$ na $PS1|temp|C_{max}$
  • Nejdříve vytvořím $T_0$ na začátek všeho a $T_{n+1}$ na konec všeho
  • tasky zdrojů vložím postupně za sebe
    • nové $s_i'=s_i+(a_i-1)*UB$ kde $a_i$ je id zdroje
    • nové $l_{ij}'=l_{ij}+(a_j-a_i)*UB$
    • každý task taky musíme omezit z $T_0$ dvěmi temporal constraints, aby byl ve svém okně
  • příkald: https://youtu.be/dhe54BPDNwo?t=4676

CP

• CSP - Constraint staisfaction problem (NP-hard)
• domain - možné hodnoty proměnné
• constrant - binární relace mezi 2 proměnnými (omezující domény)

Global constraints

• aplikovat až na konci algoritmů

Propagation and Search

• algo:
  1. pomocí constraints zkontroluji proměnné
  2. nakreslím node první proměnné
  3. nakreslím tolik větví, kolik hodnot domény má vztah s nanásledující proměnnou
  4. postupně procházím childy a postupuji stejně jako v bodu 3
  5. skončím na kreslení větví poslední proměnné
• reálné CSP používá DFS a zastaví se při nalezení prvního řešení
• příkald: https://youtu.be/SPsN60AC2jE?t=1698

AC-3 Algorithm

• Arc consistency - při vztahu z domény $x_i$ do $x_j$ existuje ke každé možné doménové hodnotě $a_i \in x_i$ existuje alespoň jedna $a_j \in x_j$, které splňuje všechny constraints
• CSP je arc consistent pokud všchny hrany jsou arc consistent
• algo:
  1. do seznamu $S$ vložíme postupně všechny arcs propojení proměnných dle constraints
  2. ze seznamu $S$ vyjmeme první dvojici proměnných $(x_i,x_j)$
  3. Revise Procedure - proměnnou $x_i$ uděláme arc consistent k proměnné $x_j$ (proškrtáme doménu $x_i$)
  4. pokud jsme doménu $x_i$ upravili (prošrtali) vložíme do $S$ všechyn závislosti na $x_i$, které ještě v $S$ nejsou (a kromě $(x_j,x_i)$)
  5. pokud v $S$ existuje další proměnná $\to$ jdeme zpět do bodu 2
• příklad: https://youtu.be/SPsN60AC2jE?t=3287