PAG Výpisky

Tasky & dekompozice

Tasky

• Při návrhu paralelního algoritmu musím prvně zadefinovat tasky, které se provádí paralelně
• Tasky se velikostně liší
• Task dependency graph - DAG - vyjadřuje závislost prováděných tasků
• Granuality - množství tasků, do kterých problém dekompunuju
• Fine-grained decomposition - velké množství tasků
• Coarse grained decomposition - malé množství tasků

Pojmy

• Degree of concurrency - Počet tasků, které mohou být prováděny paralelně
• Maximum degree of concurrency - Maximální počet tasků, které mohou být prováděny paralelně
• Average degree of concurrency
  • Průměrný počet tasků, které mohou být prováděny paralelně po dobu běhu algoritmu
  • Počet tasků / critical path length
• Degree of concurrency je závislé na granuality
• Critical Path Length - Nejdelší možná cesta, kterou běh algoritmu vykoná v rámci task dependency graphu
• Granualitu nelze snižovat do konečna - každý problém má maximální možnou granualitu
• Tasky spolu musí často komunikovat -> overhead - přílišná granualita nemusí být žádoucí

Příklad

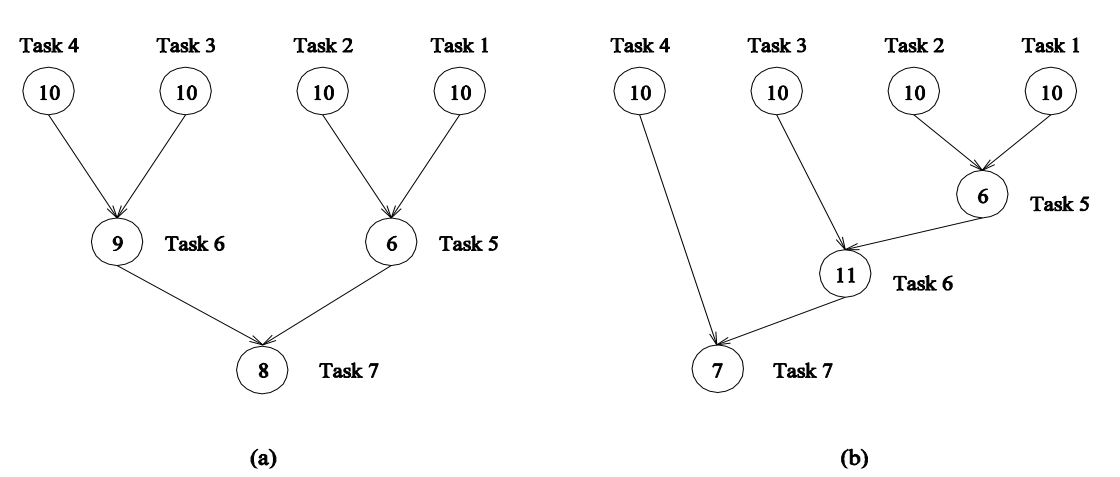
• (a)
  • Critical path length - 3 (4 nebo 3 -> 6 -> 7)
  • Shortest parallel execution time - 27
  • Processors count for minimum parallel execution time - 4
  • Maximum degree of concurrency - 4
  • Average degree of concurrency - 7/3 ❓
• (b)
  • Critical path length - 4 (2 nebo 1 -> 5 -> 6 -> 7)
  • Shortest parallel execution time - 28
  • Processors count for minimum parallel execution time - 2
  • Maximum degree of concurrency - 4
  • Average degree of concurrency - 7/4 ❓

Task Interaction Graphs

• Graf komunikace tasků
• Tasky spolu často musí komunikovat (vyměňovat data), tuto komunikaci lze znázornit grafem

Příklad

• Představme si násobení sparse matice A vektorem b
• Potřebujeme násobit pouze nenulové prvky z matice A (znázorněno černou tečkou)
• Každý task má přiřazen řádek matice A a jeden prvek vektoru b
• Např. pro provedení násobení prvního řádku se musíme doptat tasků 1,4,8 na jeho prvek z b, protože náš řádek zde obsahuje nenulové číslo a my ho potřebujeme vynásobit s příslušným prvkem z b, který náš task ale nezná

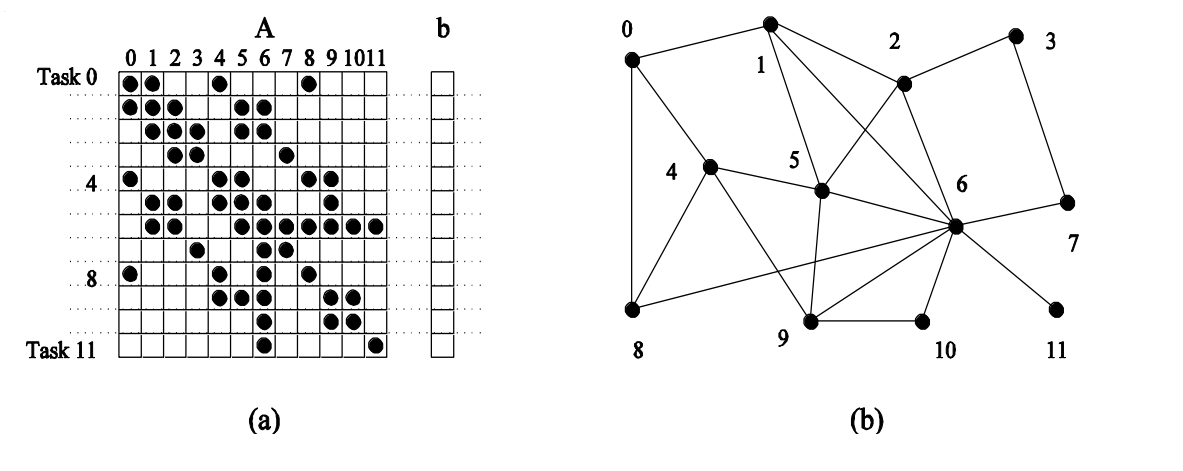
Techniky dekompozice

Jak dekomponujeme problém na tasky?

Rozlišujeme čtyři základní techniky

1. Recursive decomposition
2. Data decomposition
3. Exploratory decomposition
4. Speculative decomposition

Recursive decomposition

• Vhodná pro problémy divide-and-conquer (eg. quick sort)
• Rekursivně dekomponujeme problém dokud nedosáhneme požadované granuality

Příklad

Quicksort

• Každý sub-list může být rekurzivně zpracováván paralelně

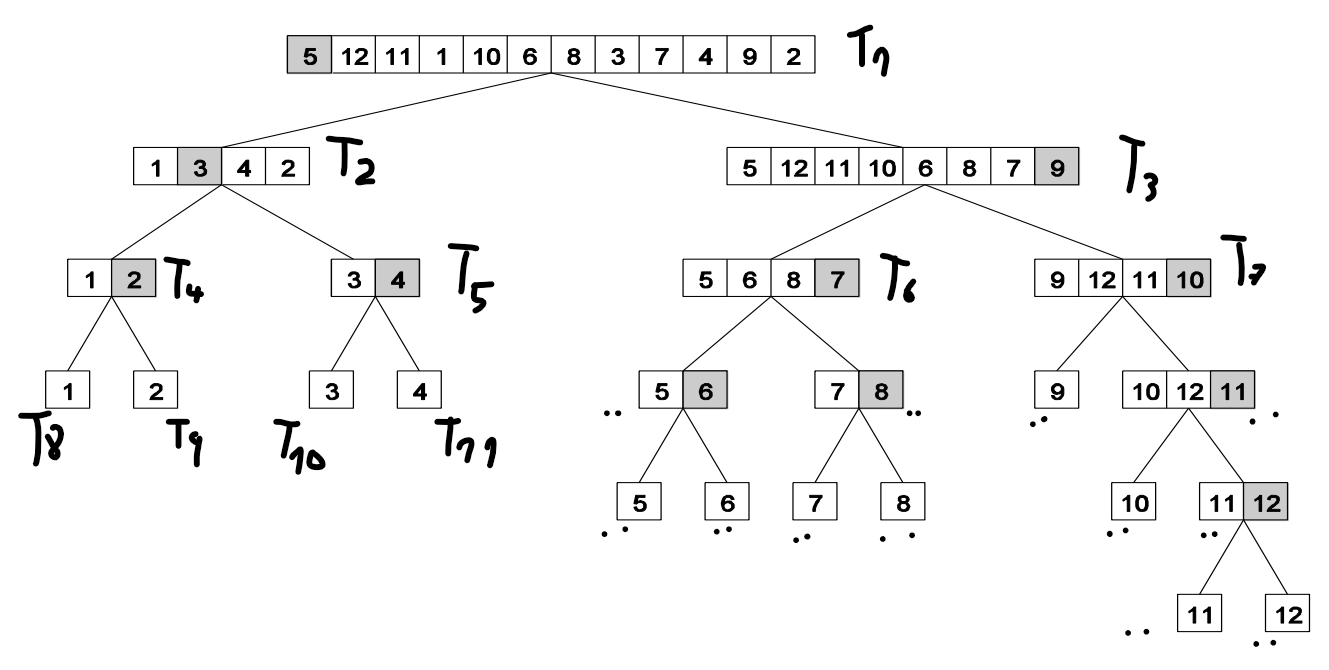
Hledání minima v listu

• Můžeme to pochopitelně dělat sériově
• Paralelně list 4,9,1,7,8,11,2,12 můžeme zpracovat následovně

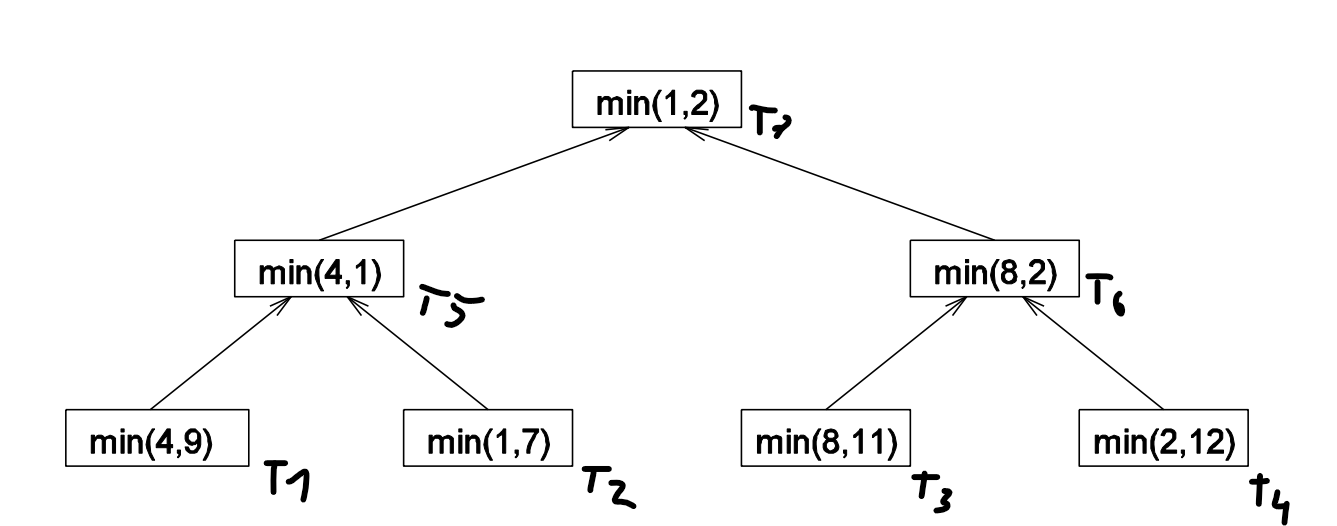
Data decomposition

• Spoléha na charakteristiku dat, s kterými algoritmus pracuje
• Dekompunujeme tyto data na jednotlivé tasky
• Volba dekompozice značně ovlivňuje výkon algoritmu
• Více přístupů
  1. Output data partitioning
  2. Input data partitioning
  3. Intermediate data partitioning

Output Data Decomposition

• Element výsledku je spočten nezávisle na ostatních výsledcích
• Pro stejný problém může existovat více output dekompozic

Příklad

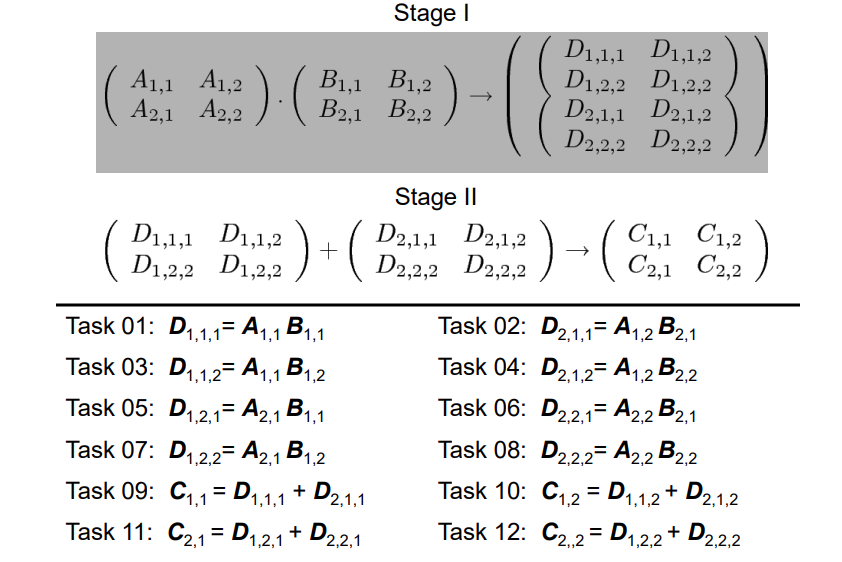
Násobení dvou matic

• Každý výsledek C je nzávislý na ostatních C

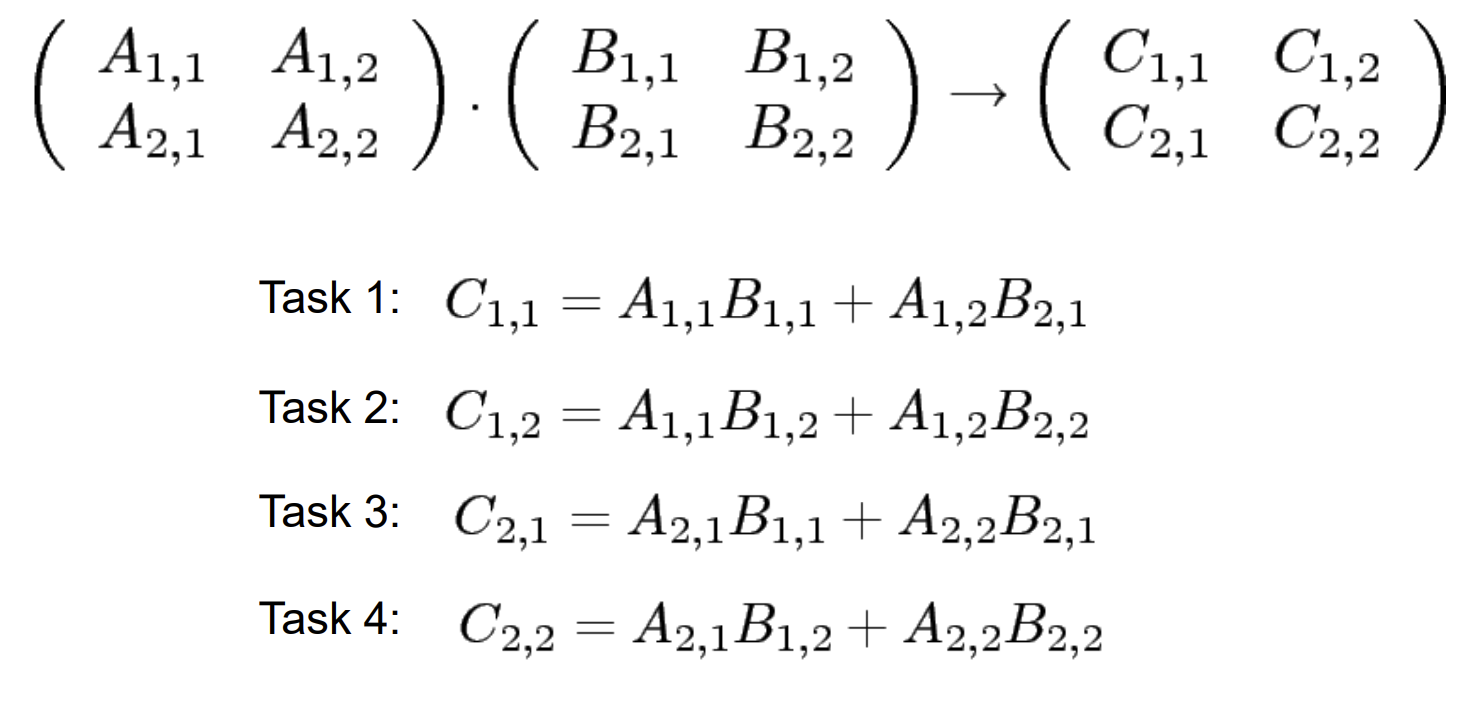
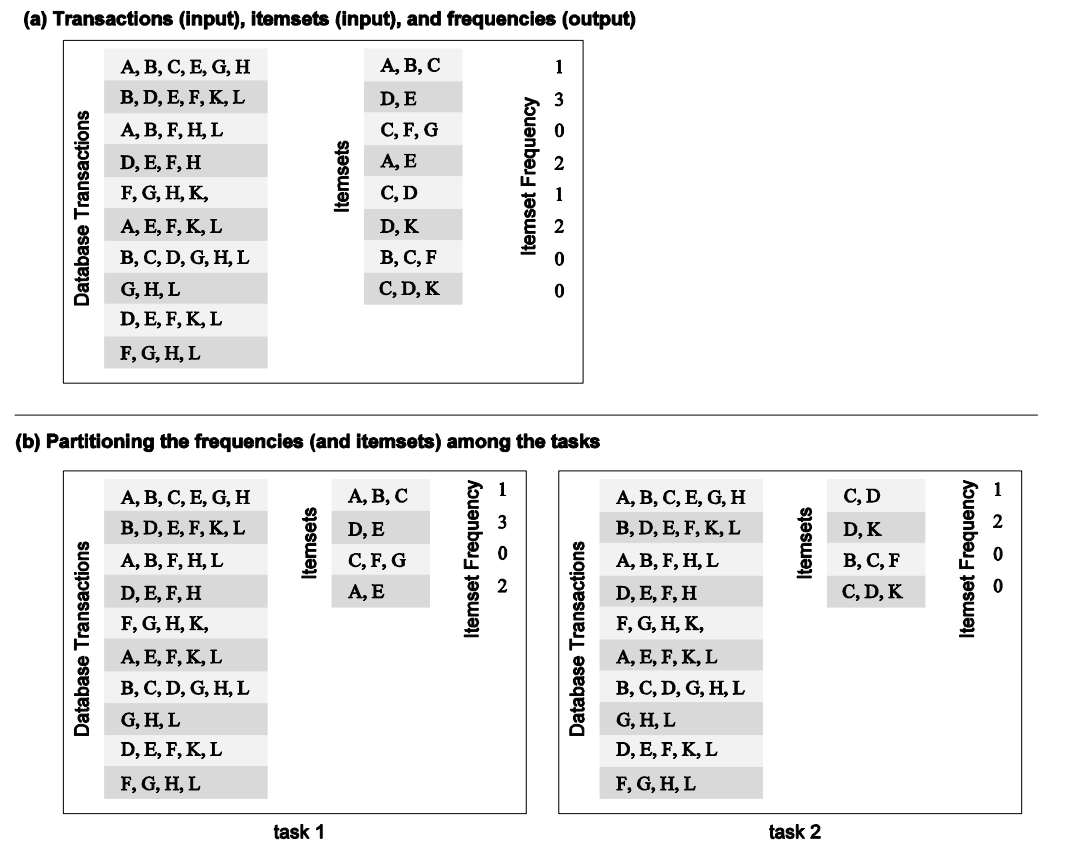
Itemset

• Chceme spočítat počet výskytů itemsetu v databázi transakcí (a)
• To můžeme dekomponovat, tak že rozdělíme itemsety do více tasků (b)
• Nepotřebujeme žádnou komunikaci mezi tasky

Input Data Partitioning

• Výstup je spočten jako funkce ze vstupu
• V mnoha případech jediná možná dekomnozice - nevíme co je výstup (např. hledání minima, sort listu)
• Tasku je přiřazena část vstupních data

Příklad

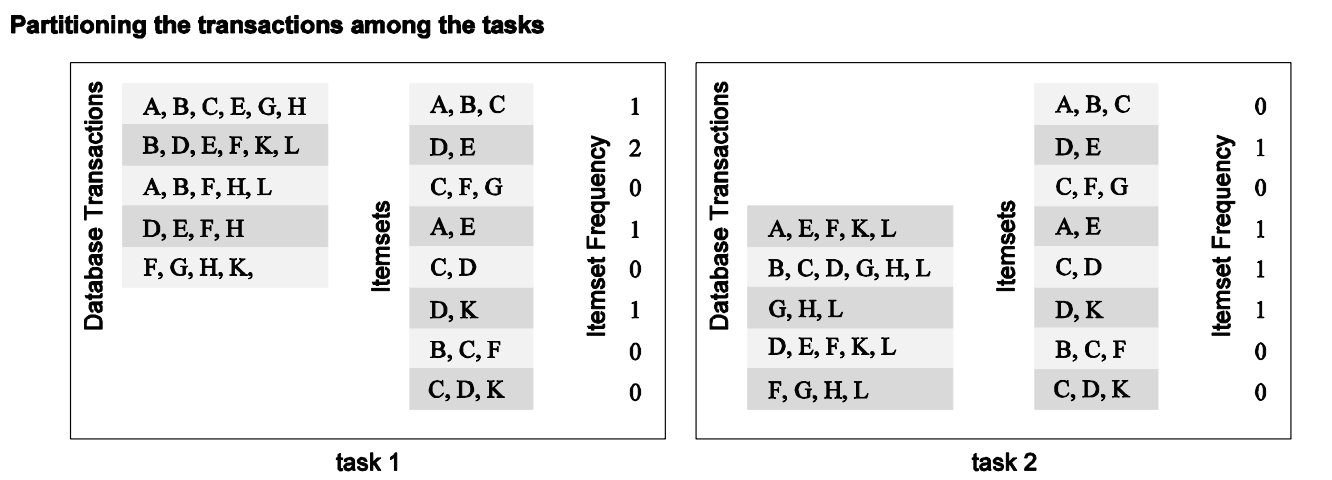
Itemset

• Rozdělíme databázi transakcí do více tasků
• Výsledky z jednotlivých tasků poté agregujeme do konečného výsledku

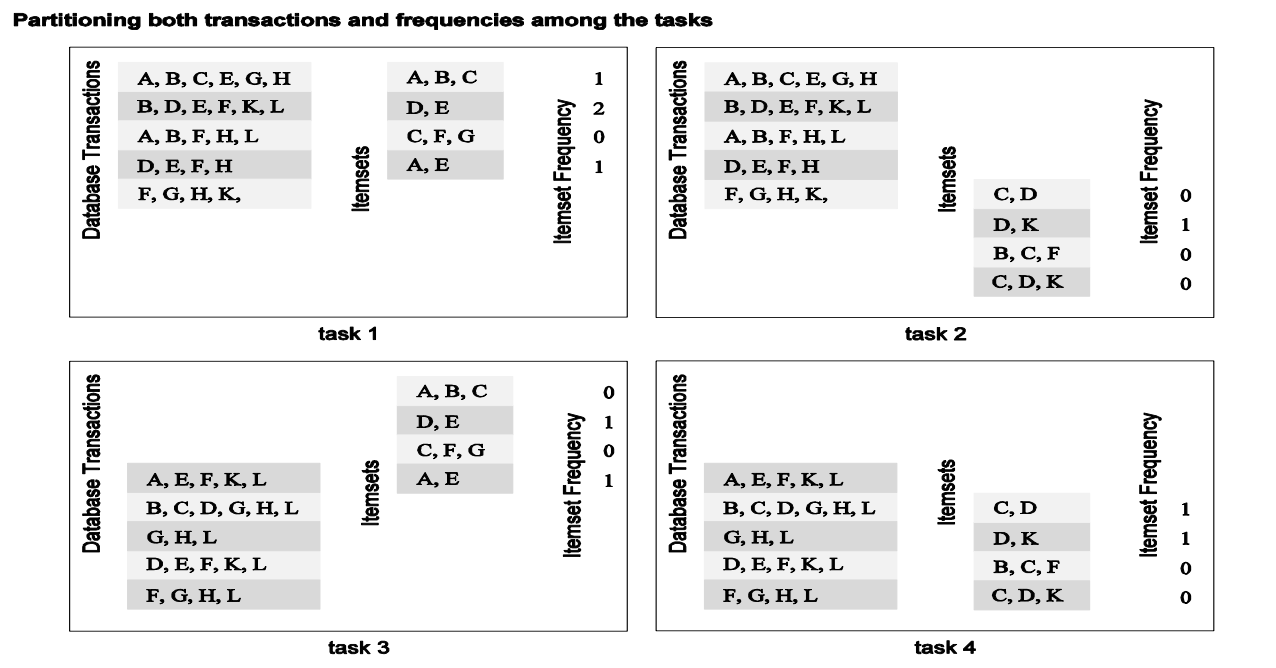
Input and Output Data Partitioning

• Kombinace obou přístupů

Intermediate Data Partitioning

• Sekvence transformací ze vstupních na výstupní data
• Počítáme “mezivýsledky” které následně tranformuje na výsledek
• Často přívější task dependency graph -> rychlejší

Exploratory Decomposition

• Dekompozice probíhá společně s průběžnými výpočty
• Použitelmé pro problémy které zahrnují explorativní hledání v prostoru řešení
  • 0/1 integer programming
  • QAP - Quadratic assignment problem
  • Theorem proving
  • Hry (např. šachy)

Příklad

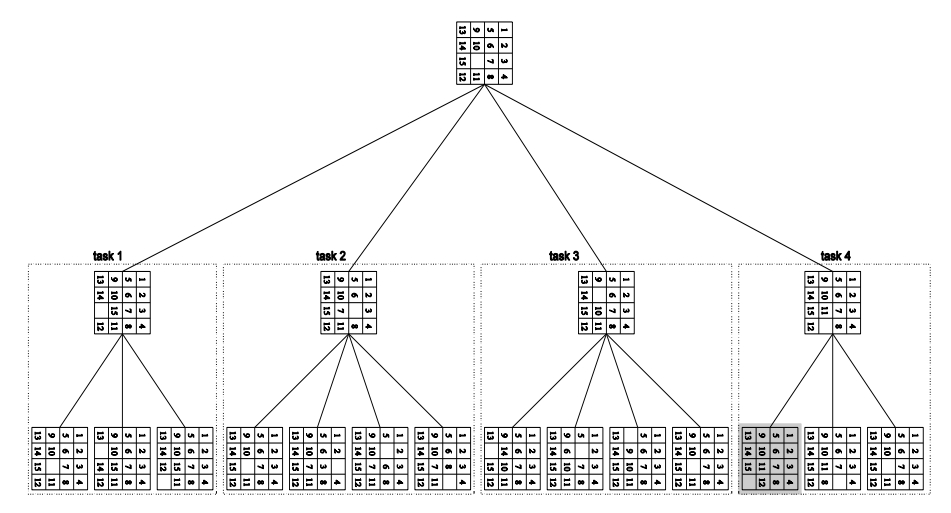
15 puzzle

• Posouváme prvky v 2d gridu tak, aby byly seřazené
• Paralelně můžeme v rámci každého tasku počítat všechny možné kroky a najít ty, které jsou správné (na obrázku je správný výsledek podbarven šedě)

Anomalous Computations

• V mnoha případech může explorativní dekompozice měnit množství vykonané práce v širokém rozsahu
• Tzn. že může stejný algoritmus být pro nějaké instance velmi rychlý (sublinear speedup) a pro jiné velmi pomalý (superlinear speedup)❓

Hybrid Decompositions

• Mix dekompozičních technik
• Často nutný pro dekompozici problémů
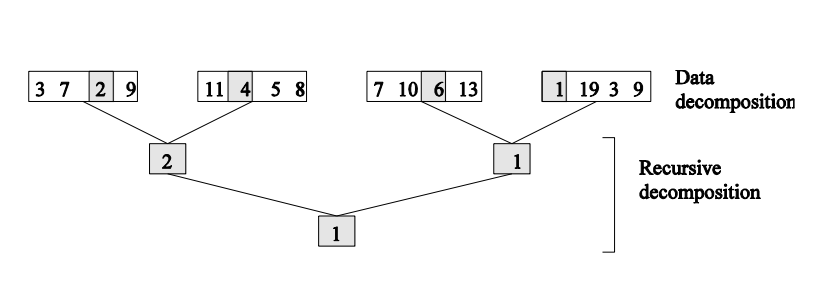
• Quicksort
  • Pouze rekurzivní dekompozice limituje maximální možnou paralelizaci
  • Lepší je použít mix data a rekurzivní dekompozice
  • To je způsobeno tím, že ❓ (hádám, že lepší než pivotovat dlouhý list je lepší to prostě rozesrat na víc procesorů rovnou)
• Hledání minima
  • Opět je lepší použít mix data a rekurzivní dekompozice

Tasky

• Problém dekomponujeme na tasky
• Charakteristictika těchto tasků značně ovlivňuje výkon algoritmu
• Faktory:
  • Task generation (Generování tasků) - Jak je tvoříme
  • Task sizes (Velikost tasků) - Jak jsou tasky velké
  • Size of data associated with tasks (Množství asociovaných dat) - Kolik dat jednotlivé tasky zpracovávají

Task generation (generování tasků)

Static task generation

• Víme, kolik tasků bude potřeba na začátku běhu algoritmu
• Např. maticové operace, grafové algortimy, zpracovávání obrázků
• Pravidelně strukturované problémy

Dynamic task generation:

• Generujeme tasky v průběhu běhu algoritmu
• Např. 15 puzzle board
• Exploratory nebo speculative decomposition

Task sizes

Uniform

• Jednotná velikost tasků

  Non-uniform

• Různě velké tasky
• Nevíme, jak budou tasky velké
• Např. discrete optimization problems

Mapping Techniques

• Tasky musíme přidělovat (mapovat) na fyzické procesory (jádra)
• Toto musí být uděláno chytře
• Minimalizujeme overheads
  • Způsobený komunikací
  • Způsobený nečiností (nepřidělenou prací) některého procesoru
• Minimalizace je optimalizační problém a často si odporuje - např. přidělením celé práce jedinému procesoru minimalizuje komunikace, ale způsobí nečinost všech ostatních procesorů

Mapping Techniques for Minimum Idling

• Musíme současně minimalizovat idling a provádět load balancing
• Pouhý loadbalancing neminimalizuje idling!
• Mapování je ovlivěno velikostí tasků, zpsůbem generování, velikostí asociovaných dat
• Případ (a) je otpimální, případ (b) není

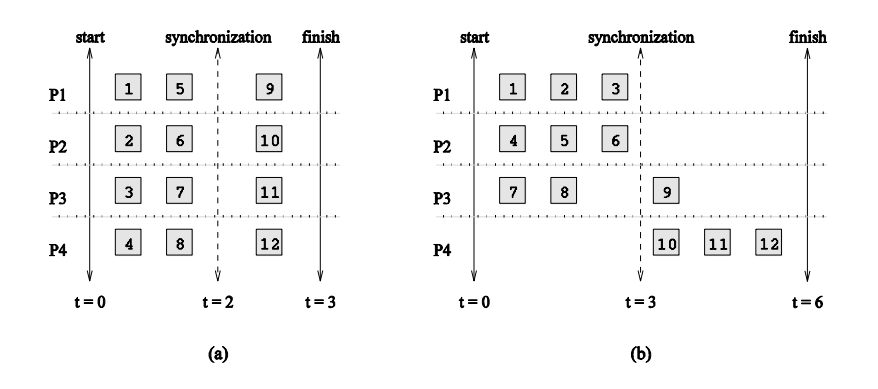
Dva základní přístupy

1. Static mapping (statické mapování)
   • Předem určíme který task bude zpracovávat jaký procesor
   • Musíme znát (nebo alespoň odhadnout) velikost tasků
   • Stejně se jedná většinou o NP-complete problém
2. Dynamic Mapping
   • Tasky přidělujeme po dobu běhu
   • Použijeme když např. generujeme tasky za běhu nebo neznáme jejich velikost

Komplexita

• Obecně se často jedná o NP-Complete problém
• Tasky mají závislosti
  • Na jeden procesor - P
  • Uniform tasky na 2 a více procesorů - NP-complete
  • Non-uniform tasky na 2 a více procesorů - NP-Complete
• Bez závislostí
  • Na jeden procesor - P
  • Non-uniform tasky na 2 a více procesorů - NP-complete
  • Uniform tasků na 2 a více procesorů - P

Schemes for Static Mapping

Mappings Based on Data Partitioning

TODO

Komunikace mezi procesory

Přehled vzorců

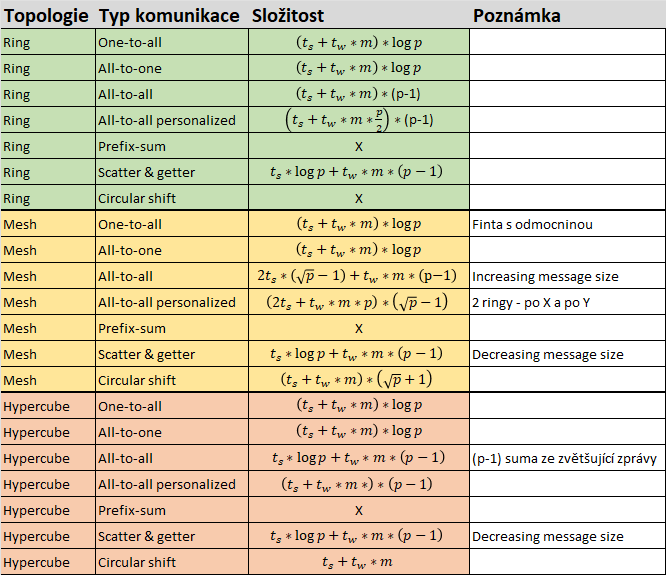
Komunikace mezi tasky

• Je třeba implementovat efektivně
• Musí vycházet z architektury použitého paralelního systému
• Skupinová komunikace je realizována jako více point-to-point zpráv
• Poslání zprávy o velikosti m zabere na nezahlcené síti t_s + t_w * m
• Tato metrika je použitá k měření rychlosti komunikace
• Pakliže potřebujeme počítat se zahlcenou sítí -> zvyšujeme t_w
• Předpokládáme, že komunikační síť je obousměrná a jednoportová

One-to-All Broadcat

• Jeden procesor zasílá data o velikosti m všem ostatním procesorů

All-to-One Reduction

• Všechny procesory zasílají zprávu o velikosti m jednomu procesoru
• Tyto data jsou na “centrálním” procesoru agregovány použitím asociativní operace (např. plus, minimum)

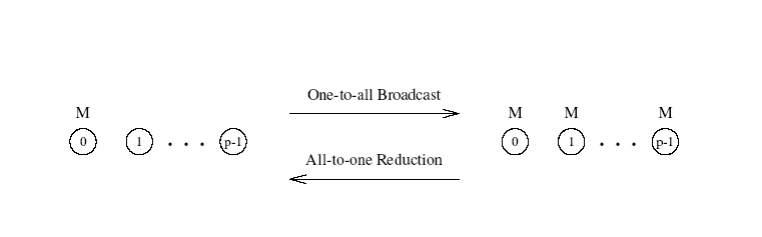
One-to-All Broadcats / All-to-One Reduction

Ring

• Broadcast - K poslání p - 1 zpráv použijeme rekurzivní dvojení (recursive doubling)
  • Zdrojový procesor odešle zprávu na první procesor. Nyní mají oba dva tyto procesory na starosti pouze půlku ze všech procesorů

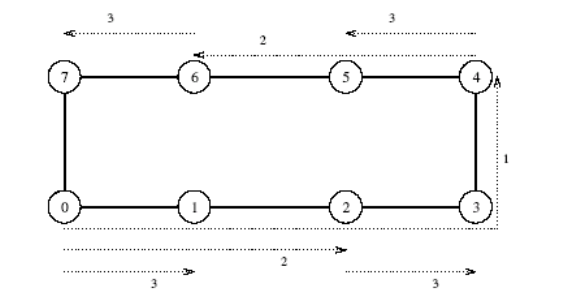
• Redukce - Obdobný princip ale naopak

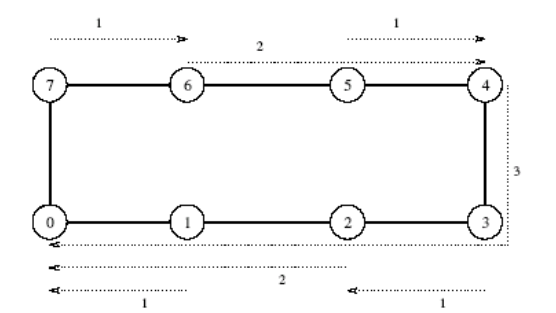
Mesh

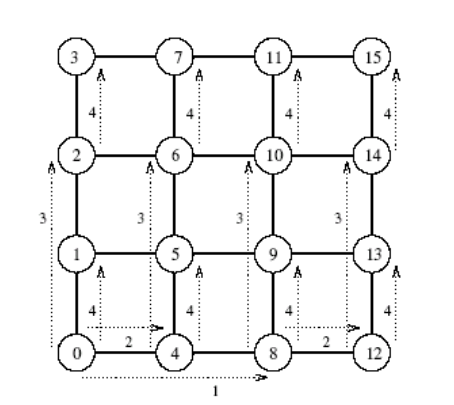
• Čtvercová matice p procesorů má sqrt(p) sloupců a řádků
• Broadcast a redukce má dva kroky
  1. Rozšíříme zprávu po řádce
  2. Následně posíláme zprávu paralelně po sloupcích
• Zobecnění tohoto postupu funguje ve více dimensích

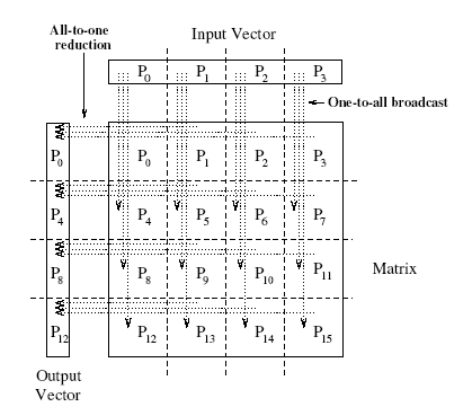
Příklad

• Násobíme matici A vektorem v
• Musíme provést nejprve one-to-all broadcast a následně all-to-one redukci
• Čárkované šipky znázorňují směr komunikae
• Vidíme, že každý procesor P má přidělený čtvercový kus dat matice A a jeden prvek vektoru v
• Pro provedení výpočtu musí tedy kupříkladu procesor P_0 poslat svůj prvek vektoru A na procesor P_4, P_8 a P_12
• Následně kupříkladu procesory P_1, P_2, P_3 zaslšou data procesoru P_0 který provede agregaci sečtením

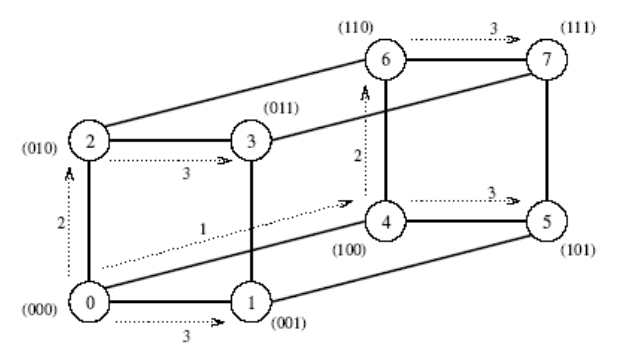
Hypercube

• K hypercube s 2^d nody můžeme přistupovat jako k d-dimensionální meshi (dva vrcholy na dimensi)
• Mesh algoritmus můžeme generalizovat k použití na hypercube s d = log(p) kroky

Algoritmy pro broadcasts a reductions

• Všechny výše zmíněné příklady komunikace (viz. obrázky) používají stejný princip
• Algoritmus může být snadno přizpůsoben i pro další topologie

One to all (hypercube)

All to one (hypercube)

Cost analysis

• Broadcast i redukce potřebuje log p point-to-point přenosů, kde kadžá stojí poslat t_s + t_w*m
• Celková cena je tedy: T = (t_s + t_w*m) * log(p)

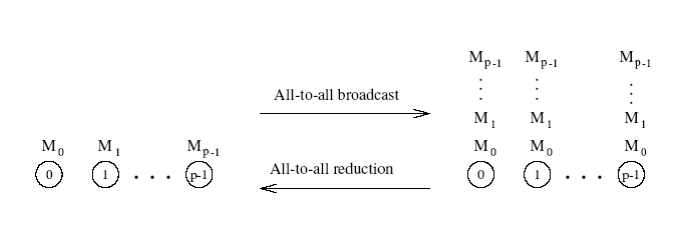
All-to-All Broadcats

• Generalizace přechozího, kde každý procesor vysílá i příjímá zprávy současně
• V rámci procesu každý procesor pošle stejnou zprávu velikosti m všem ostatním procesorům
• Různé procesy mohou posílat různé zprávy

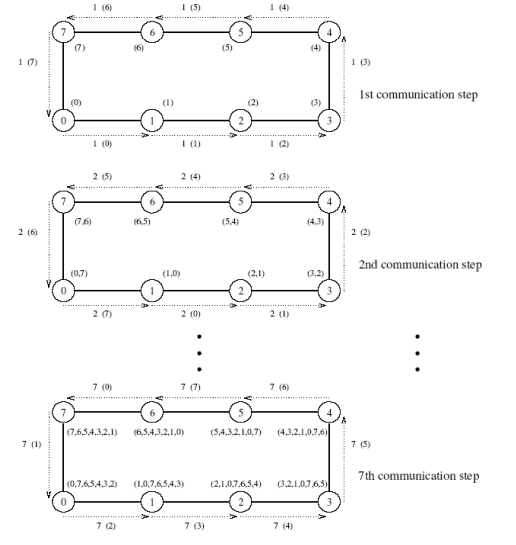
Ring

• V prvním kroku zašle každý procesor svoji zprávu sousedícímu procesoru pro směru hodinových ručiček
• V každém dalších krocích vždy přepošle data, které obdržel od jednoho souseda druhému sousedu
• Algoritmus končí po p-1 krocích

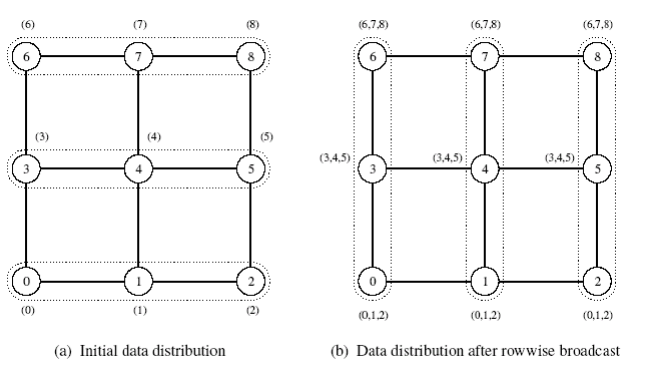
Mesh

• Dva kroky
  1. Každá řádka mřížky provede all-to-all broadcast mezi sebou “lineárně” - každý node získa sqrt(p) zpráv
  2. Každý node rozšíří přijaté zprávy jako zprávu velikosti m*sqrt(p) po sloupci

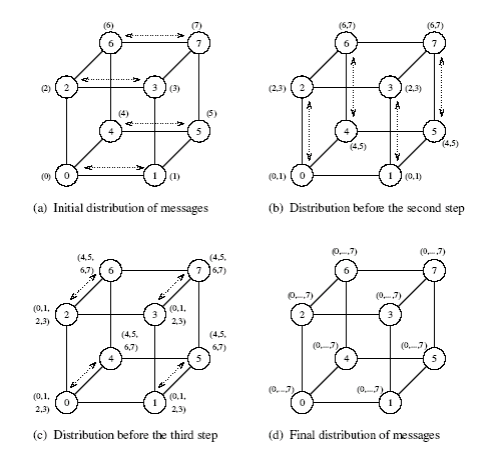
Hypercube

• Zobecnění mesh algoritmu pro log p dimensí
• Velikost zpráv se zdvojnásobuje s každým z log(p) kroků

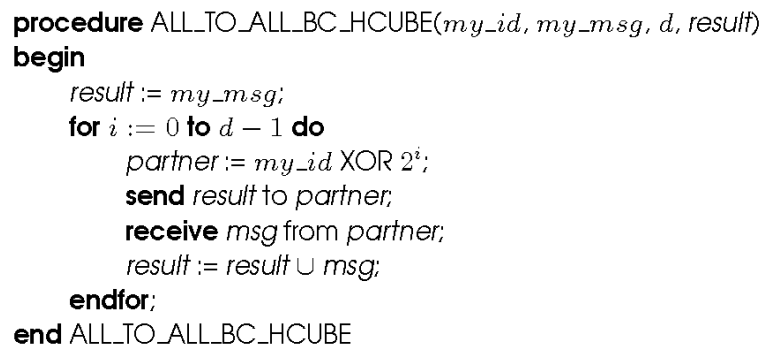
All-to-All Reduction

• Podobné jako pro all-to-all broadcast, pořadí je opačné
• Při přijetí zprávy ji musí node zkombinovat s lokální kopií zprávy, která má stejnou destinaci jako zpráva přijatá
• Po zkombinování je zpráva zaslána sousedovi

Cost analysis

• Kruh - T = (t_s + t_w * m)*(p-1)
• Mesh - T = 2 * t_s * (sqrt(p) - 1) + t_w * m * (p-1)
• Hypercube - T = t_s * log(p) + t_w * m * (p-1)

All-reduce

• Kadžý node začíná s bufferem o velikosti m
• Výsledkem je buffer velikosti m na každém nodu, který obsahuje agregovaná data ze všech nodů za pomocí asociativní operace
• Shodné jako all-to-one reduction s následným one-to-all broadcastem (to je méně efektivní ❓)
• Vhodnější je použít all-to-all broadcast, kde se nezvětšuje velikost zprávy
• T = (t_s + t_w * m) * log(p)
• Rozdíl od all-to-all - neprobíhá p souběžných all-to-one redukcí, každá s jiným cílem výsledku

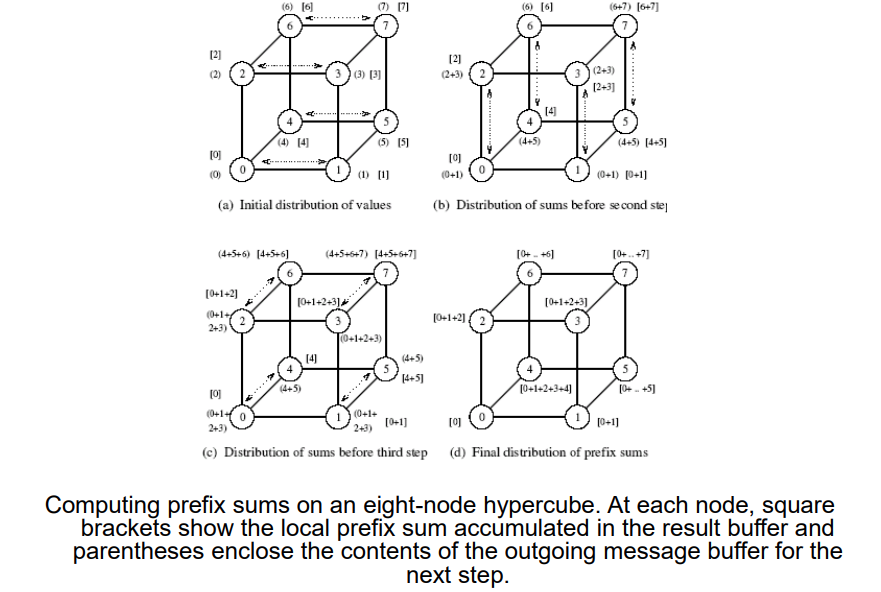
Prefix-Sum

• Mějme p čísel n_0, n_1,…,n_p-1 (každé na jiném nodu), chceme spočíst sumu těchto čísel pro od 0 po k, kde k je v rosahu 0 až p-1
• Jinými slovy na každym nodu chceme sumu z čísel n_x kde x \el {0,…,k} a k je index toho nodu
• Suma nahradí prvek n_k

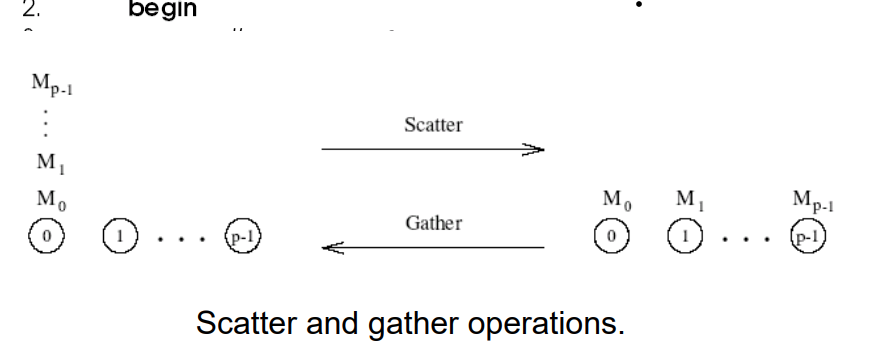
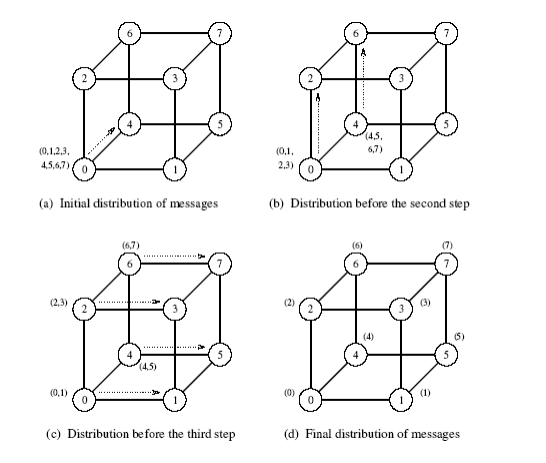
Scatter and Gather

• Dva kroky
  1. Scatter - Jeden node zašle unikátní zprávu velikosti m všem ostatním nodům (one-to-all personalized)
  2. Getter - Jeden node sbírá unikátní zprávy od všech ostatních
• Ačkoli je principielně scatter operace jiná než broadcast, algoritmicky se podobají až na velikost zprávy (zprávy se změnšují u scatteru, ale zůstávají stejné u broadcastu)
• Getter operace je inverzní operací scatteru

Cost analysis

• Dochází k log(p) kroků, v každém kroku se půlí velikost zprávy stejně tak jako pomyslná velikost zbývajího stroje
• T = t_s * log(p) + t_w * m * (p-1)
• Toto platí pro linární pole a 2-D mesh
• Tyto časy jsou asymptociky optimální ve velikosti zpráv

All-to-All Personalized Communication

• Jinak známo jako total exchange
• Každý node má odlišnou zprávu velikosti m pro každý další node
• Nezaměňovat s all-to-all broadcastem, kde každý node posílá stejnou zprávu!

Příklad

• Transponování matice
• Každý procesor obsahuje řádek matice
• Transponování tak vyžaduje all-to-all personalizovanou komunikaci

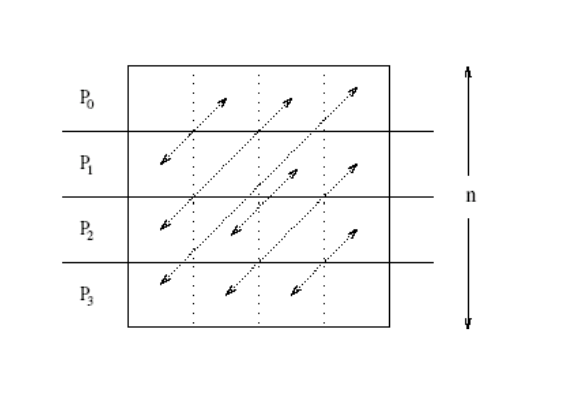
Ring

• Postup:
  1. Každý node pošle všechna data jako jednu zprávu o velikosti m * (p-1) jednomu ze sousedů
  2. Každý node si vybere zprávu určenou pro něj a zbytek pošle dál
• Algortimus končí za p - 1 kroků
• Zpráva se každý další krok zmenšuje o m

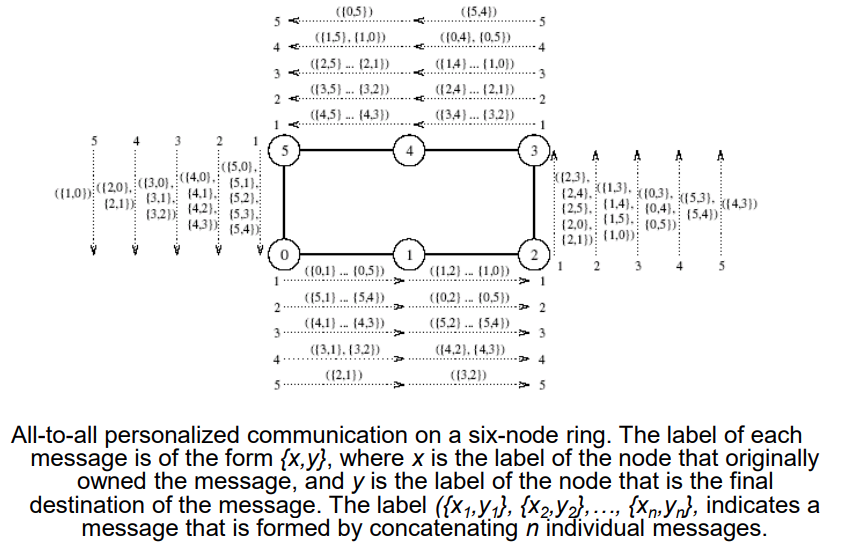
Cost

• Máme p -1 kroků
• v i-tém kroku je velikost zprávy m * (p - i)
• 
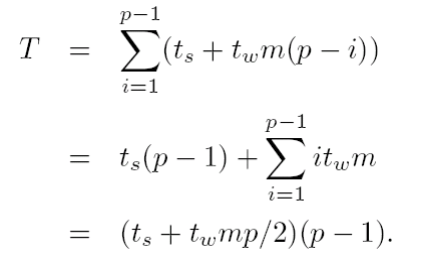
• Člen t_w může být dělen 2 pomocí obousměrné komunikace ❓

Mesh

• Postup:
  1. Každý uzel nejprve seskupí svých p zpráv podle sloupců jejich cílových nodů
  2. Na všech řádcích se nezávisle provede All-to-all personalised komunikace se seskupenými zpávami o velikosti m * sqrt(p)
  3. Zprávy na nodech jsou znovu seskupeny tentokrát podle řádků jejich cílových nodů
  4. Na všech sloupcích se nezávisle provede All-to-all personalised komunikace se seskupenými zpávami o velikosti m * sqrt(p)

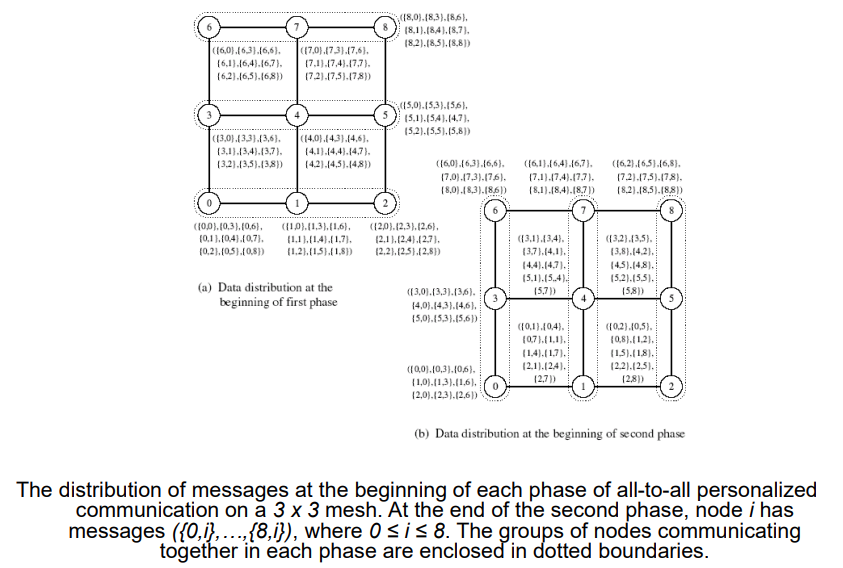
Cost

• První fáze je totožná s ringem se sqrt(p) procesory tj. (t_s + t_w * m * p / 2)*(sqrt(p) - 1)
• Druhá fáze je cenově shodná s první
• 
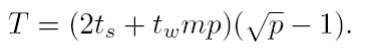
• Čas pro seskupení je výrazně menší než komunikační čas

Hypercube

• Zobecnění mesh algoritmu na log(p) kroků
• V každém kroku all-to-all pernoslized komunikace drží každý node p zpráv o velikosti m
• Během komunikace v dané dimensi pošle zašle každý node p/2 zpráv jako jednu seskupenou zprávu
• Před každým dalším krokem musí znovu provést seskupení zpráv

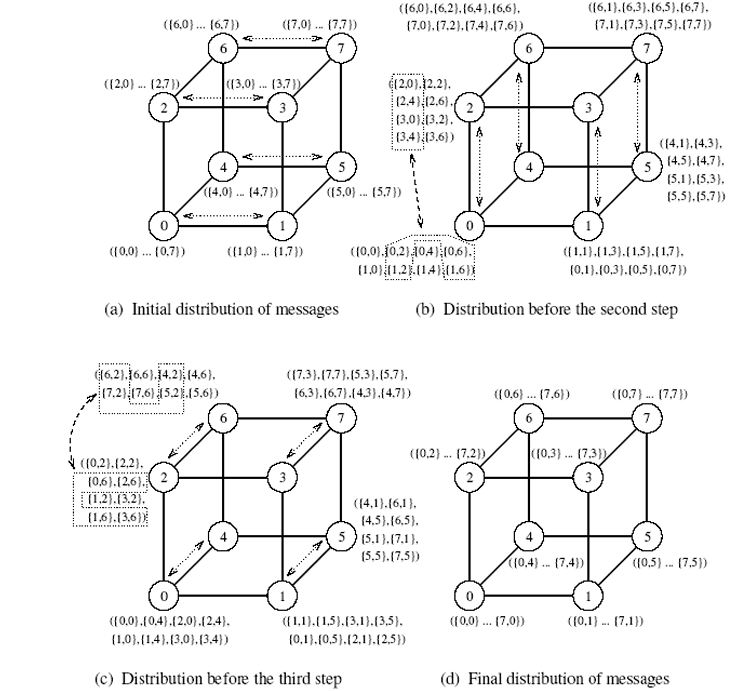
Cost

• Máme log(p) iterací a m * p / 2 iterací
• 
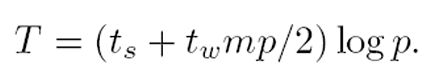
• Toto není optimální!
• Každý z p nodů posílá a přijímá m * (p-1) slov, průměrná vzdálenost na hypercube mezi dvěma nody je log(p) / 2 a nachází se zde (p * log(p) / 2) spojení
• 

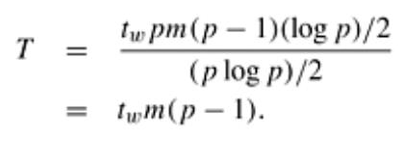
Optimální algoritmus

• Každý node provede p - 1 komunikaních kroků a vymění si m slov s jiným nodem v každém kroku
• Node si vybírá protistranu komunikace v každém kroku tak, aby nedošlo k zahlcení sítě
• V j-tém kroku si node i vymění zprávy s nodem i XOR j

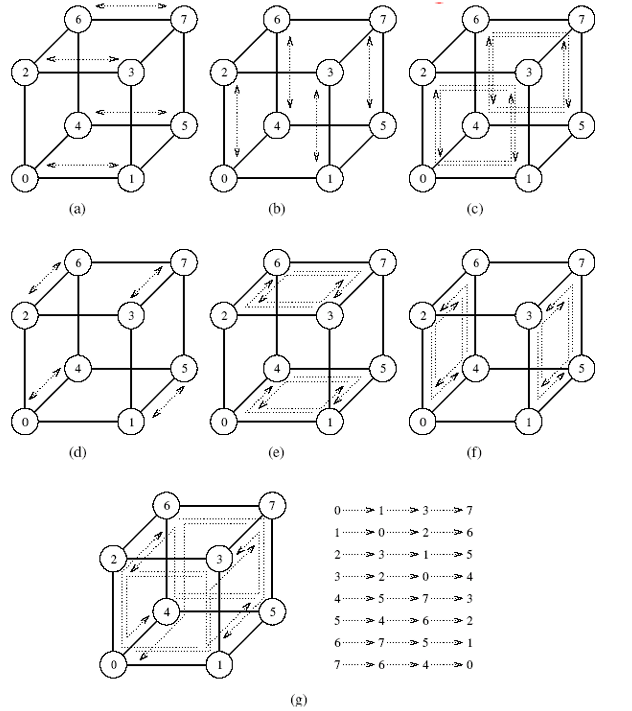
Cost

• Dochází k p - 1 krokům
• V každém kroku se přenese m slov bez zahlcení
• 
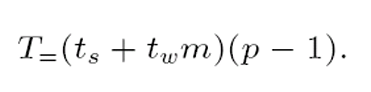
• Optimální ve velikosti zprávy

Circular shift

• Permutace, ve kterém i-tý node pošle zprávu nodu (i + q) mod p
• 0 <= q <= p

Ring

• Lze provést v min{p, q-p} komunikacích se sousedem

Mesh

• Všechny nody pošlou zprávu sousedovi v jednom směru a následně i v druhém směru
• 

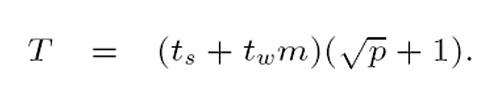
Hypercube

TODO

Summary

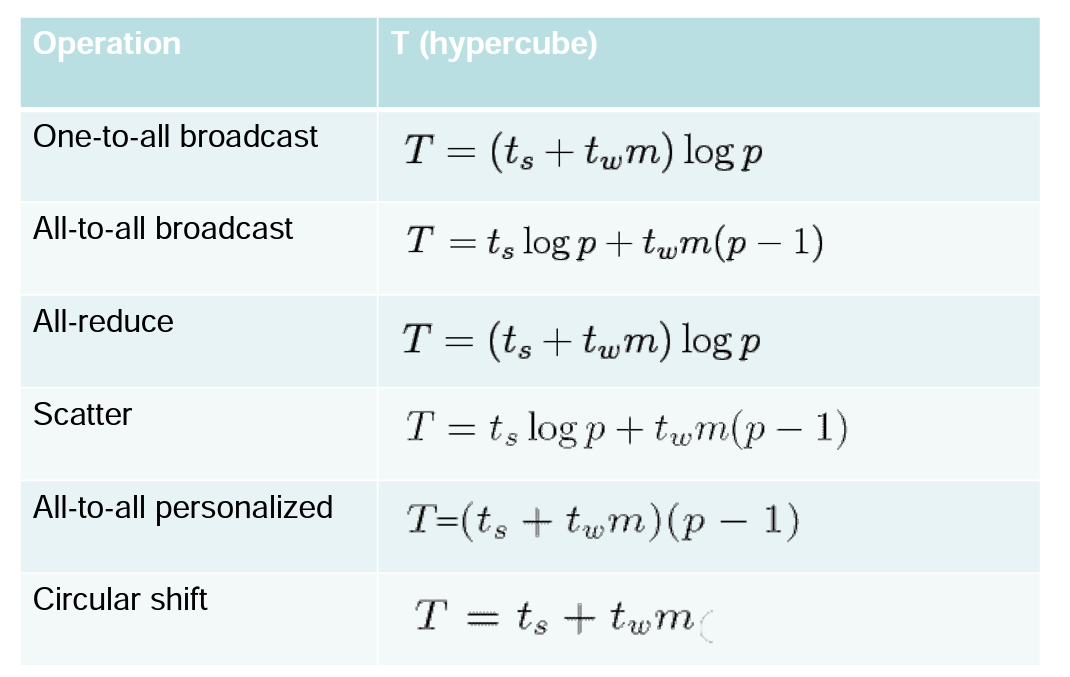
Analytical model

• Sekvenční algoritmy
  • Vyhodnocujeme asymptotickou dobu běhu nezávisle na platformě
  • Doba běhu je závislá na velikosti vtupu
• Paralelní algoritmy
  • Vyhodnocujeme dobu běhu v závislosti na platformě
  • Doba běhu je závislá na velikosti vstupu, počtu procesorů a komunikačních parametrech
• Dva-krát tolik procesorů neznamená dvakrát rychlejší běh <= overheads (komunikace, idling, zahlcení sítě, atd.)

Metriky

Execution time

• Sériové algoritmy
  • Doba běhu algoritmu od začátku do konce
  • Značíme T_S
• Paralelní algortimy
  • Doba běhu od začátku práce prvního procesoru do skončení posledního procesoru
  • Značíme T_P

Total Parallel Overhead

• T_all = p * T_p Celkový čas všech procesorů
• Celkový overhead
  • Čas strávený všemi procesory na neužitečné práci
  • Značíme T_o
  • T_o = T_all - T_S = p * T_P - T_S

Speedup

• 
• Poměr mezi časem strávený sériovým algoritmem a paralelním algoritmem s p stejnými procesory
• Pro jeden problém může existovat více různě výkoných (asymptociká složitost) sériových algoritmů s rozdílou mírou možné paralelizace
• Pro výpočet speedupu používáme vždy nevýkonější možný
• Speed může být nejméně 0 - parallení program nedoběhne
• Teorticky může být speedup maximálně p - tj. nemůžeme zrychlit o víc než kolik přiřadíme výpočetních jednotek
• V praxi toto ale neplatí - jeden procesor může strávit výpočetem méně než T_S / p = superlinear speedup

Superlinear speedup

• Paralelní algoritmus může ve výsledku odvést méně práce než jeho sériový protějšek
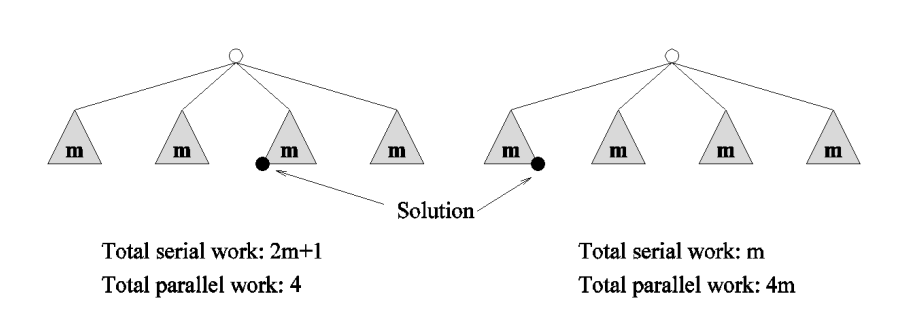
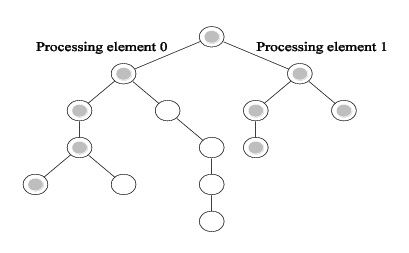
• Příklad: Hledání prvku ve stromu pomocí DFS
  • Hledáme prvek nejvíce v pravo dole
  • Sériový program prohledá celý strom
  • Paralelní rozdělí práci na dva podstromy mezi dva procesory a zastaví se dříve, než je prohledán celý strom = méně práce

Amdahl’s Law

• Každý algoritmus obsahuje část, která je
  • Přirozeně sekvenční β
  • Přirozeně paralelní (1 - β)
• Speedup je limitován přirozeně sekvenční částí
• Amdahl’s Law definije maximální možný teoretický speedup (ignoruje overhead a cenu komunikace)
• Sériová část je spočtena jako β * T_S
• Paralelní část je spočtena jako (1-β) * T_S / p
• Z toho plyne, že T_P = β * T_S + (1-β) * T_S / p
• Pro speedup potom platí:
• 

Efficiency

• 
• Poměr času, kdy je procesor efektivně vytížen
• 

Cost

• 
• Suma času, po kterou procesory provádely výpočty
• Paralelní systému je cost optimal, pokud je cost řešení problému na paralelním počítači asymptoticky shodný se sériovým costem
• Protože je pro cost optimal systémy

Efekt granuality na výkon

• Velmi často menší množství přidělených procesorů zvyšuje výkon paralelního systému
• Scalling down - přidělení menšího než maximálního možného množství procesorů pro paralelní algoritmus
• Scalling down - naivní implementace = V původním případě považujeme všechny procesory jako virtuální procesory a ty přidělíme na “scaled-down” procesory
• Vzhledem k tomu že se množství procesních elemtnů snížilo o n / p, výpočty na zbylých procesorech se zvýší o n / p
• Cena komunikace mezi procesory se však nezvýší o tento faktor, protože některé virutální procesory přiřazené na stejný procesor spolu mohou komunikovat “zdarma” - toto je základní důvod zrychlení při snížení granuality

Scalability of Parallel Systems

• Jak můžeme extrapolovat data o výkonu z malých problémů a systémů na velké problémy a systémy?

Scaling Characteristics

• Víme, že nebo také
• Celková funkce overheadu T_o je roustoucí funkcí p
• Pro danou velikost problému (tj. T_S se nemění), jakmile zvýšíme počet procesorů p, T_o roste a celková efektivita algoritmu klesá
• To platí vdžy
• Funkce T_o je funkcí jak velikost problému (n -> T_S), tak počtu procesorů p
• V mnohda případech roste T_o sublineárně vzhledem k T_S
• V takových případech roste efektivita když je zvětšeno n při zachování počtu procesorů p
• To znamená že můžeme společně zvětšovat velikost problému n společně počtem proceosrů p při zachování kontantní efektivity
• Tyto systémy nazýváme scalable
• Scalability a cost-effectivity jsou propojené veličiny
• Scalable systém může být vždy učiněn cost-optimal (Θ(1)), když vybereme správně počet procesorů p vzhledem k velikosti problému
• Když pro stejnou velikost problému zvyšujeme počet procesorů p => efektivita klesá

Isoefficiency

• Jaký je poměr zvětšení velikosti problému k počtu procesorů aby zůstala efektivita fixní?
• Tento poměr určuje škálovatelnost systému
• Čím “pomalejší”, tím lepší
• W - počet operací v nejlepším sériovém algoritmu